Глава II
МЕТОД ПРОСТЫХ СИСТЕМ АЛЬТЕРНАТИВ
 2.1 Основные понятия
2.1 Основные понятия
 2.2 Логический вывод в системах альтернатив
2.2 Логический вывод в системах альтернатив
 2.3 Модули знаний в системах альтернатив
2.3 Модули знаний в системах альтернатив
Модуль альтернативы • Модуль несовместимости •
Модуль запрета • Модуль импликации •
Модуль продукции • Структурирование систем альтернатив
 2.4 Реализация процедуры логического вывода
2.4 Реализация процедуры логического вывода
 2.5 Модифицированные системы альтернатив
2.5 Модифицированные системы альтернатив
| |
Веб-версия диссертации размещена автором на www.park.glossary.ru.
Копии веб-версии на иных сайтах заведомо получены и размещены с нарушением
авторских прав, без согласия и без отвественности автора. |
Простые системы альтернатив есть метод организации и
обработки данных в интересах решения переборных задач. В АСИЗ
задачи такого рода возникают при реализации блока анализа
протоколов. Кроме того, простые системы альтернатив допускают
использование в качестве метода реализации баз знаний (п. 1.2.5).
В настоящей главе для обозначения множеств используются
прописные буквы латинского алфавита: A, B и т.д. Те же строчные
буквы (если это не вызывает недоразумений) обозначают элементы
множеств. Все рассматриваемые множества являются конечными.
2.1 Основные понятия
Притягательной чертой продукционных систем является
простота и универсальность их базовой конструкции. Существует и
другая, быть может, еще более простая базовая конструкция,
позволяющая эффективно проводить логический вывод. Этой
конструкцией является альтернатива, которая задает исчерпывающую
классификацию проблемных ситуаций с некоторой точки зрения.
Альтернативы также обладают свойством универсальности и, в
принципе, позволяют строить базу знаний путем систематического
накопления различных классификаций.
Определение 2.1
Простой системой альтернатив или ПА-системой называется
тройка конечных множеств (S,C,A), где S - множество основных
фактов, C - множество вспомогательных фактов (причем S ∪ C = ∅),
A - совокупность подмножеств из S ∪ C. Элементы множества A
называются альтернативами. 
| Соглашение. |
| (1) |
В дальнейшем для обозначения объединенного множества фактов
будем использовать символ "H".
|
| (2) |
Не ограничивая общности множества S, C и H можно считать
упорядоченными
S = {s1, ..., sk},
C = {c1, ..., cn},
H = {s1, ..., sk, c1, ..., cn}.
|
| (3) |
Для обозначения альтернатив будем использовать специальные скобки:
<h1, ..., hm> ∈ A.
|
| (4) |
Будем рассматривать только такие ПА-системы, в которых
каждый факт входит, по крайней мере, в одну альтернативу,
что позволяет задавать ПА-системы простым перечислением
альтернатив. 
|
Пусть R - ПА-система (S,C,A). Рассмотрим множество
характеристических функций f : H → {0,1}.
Определение 2.2
Будем говорить, что характеристическая функция f
удовлетворяет ПА-системе R, если для любой альтернативы
<h1, ..., hm> из A имеет место равенство
f(h1) + ... + f(hm) = 1
Множество функций, удовлетворяющих ПА-системе R, будем
обозначать F(R). 
Если f - характеристическая функция, заданная на множестве
X, и Y - подмножество X, то функция f однозначно определяет
подмножество f(Y). f(Y) = {x ∈ Y | f(x) = 1}. Используя это
обозначение, определим для ПА-системы R два множества.
Определение 2.3
Q(R) = {f(H) | f ∈ F(R)},
K(R) = {f(S) | f ∈ F(R)}.
Множество K(R) называется классом распознавания ПА-системы. 
Элементы класса распознавания описывают (путем
перечисления) допустимые комбинации основных фактов. Очевидно,
что K(R) = {S ∪ q | q ∈ Q(R)}.
Рассмотрим задачу построения класса распознавания по
известной системе альтернатив.
Задача 2.4 (Прямая задача)
Дано. ПА-система R = (S,C,A).
Требуется. Построить класс распознавания K(R). 
Приведем подход к решению задачи 2.4. Обозначим:
E - вектор размерности ||A||, состоящий из всех единиц,
X - вектор неизвестных размерности p = ||H||:
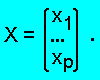
где x - некоторый фиксированный символ. Каждый элемент вектора X
может принимать значения 0 или 1. По множеству A построим
матрицу M размерности ||A|| х ||H||.
Для каждой альтернативы a матрица содержит строку
m1 ... mp, где
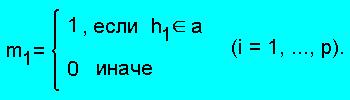
По построению система булевых целочисленных уравнений
MX = E содержит все соотношения, которым должны удовлетворять
функции из множества F(R). Таким образом, система MX = E, с
учетом разбиения множества неизвестных на два класса
{xi | i ≤ ||S||}
и
{xi | i > ||S||},
является эквивалентным представлением системы альтернатив.
Каждое решение
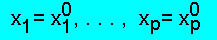 системы MX = E взаимно однозначно определяет характеристическую
функцию f, удовлетворяющую ПА-системе,
системы MX = E взаимно однозначно определяет характеристическую
функцию f, удовлетворяющую ПА-системе,
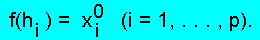 Поэтому для нахождения искомого класса распознавания достаточно
воспользоваться формулами, заложенными в определении 2.3.
Поэтому для нахождения искомого класса распознавания достаточно
воспользоваться формулами, заложенными в определении 2.3.
Отметим, что описанный подход к решению прямой задачи позволяет
находить не только класс распознавания, но и множество Q(R).
В интересах реализации баз знаний интерес представляет
задача построения ПА-системы с заданным классом распознавания.
Задача 2.5 (Обратная задача)
Пусть S = {s1, ..., sk} - исходное множество основных
фактов. Кроме того, известно множество K0 ⊂ 2S.
Требуется построить ПА-систему R такую, что K(R) = K0.

Покажем, что обратная задача разрешима.
Прежде всего построим множество вспомогательных фактов.
Положим C - множество всевозможных функций c : S → {0,1}.
Очевидно, что ||С|| = 2k.
Построим ПА-систему R1 = (S,C,A1), в которой
A1 = {C, a1, ..., ak}.
Здесь C - альтернатива, содержащая все вспомогательные
факты, а состав фактов альтернативы aj (j=1,..., k)
определяется по формуле
{sj} ∪ {c ∈ C | c(sj) = 0}.
Каждому вспомогательному факту c сопоставим функцию
fc : H → {0,1}
следующим образом:
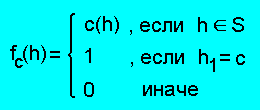
Свойство системы R1 сформулируем в виде леммы.
Лемма 2.6
F(R1) = {fс | c ∈ C}.
Доказательство проведем в два этапа.
(1) Пусть c - произвольный элемент из C. Покажем, что fc
удовлетворяет ПА-системе R1.
Альтернативе C функция fc удовлетворяет по построению.
Рассмотрим альтернативу a1. Теоретически для fc возможны два
варианта: либо fc(s1) = 0, либо fc(s1) = 1. В первом случае
равенство из определения 2.2 выполняется за счет значения fc(c).
Во втором случае c(s1) = 1 и, следовательно, c ∈ a1, т.е.
равенство из определения 2.2 выполняется за счет значения
fc(s1). Аналогично рассматриваются и остальные альтернативы.
Таким образом,
{fc | c ∈ C} ⊂ F(R1).
(2) Пусть f ∈ F(R1). Из альтернативы C следует, что
f(c) = 1 для некоторого c. Предположим, что f ≠ fc. Это означает
существование некоторого основного факта sj такого, что
f(sj) ≠ c(sj). Теоретически для функции f возможны два варианта:
либо f(sj) = 0 и тогда c(sj) = 1,
либо f(sj) = 1 и тогда c(sj) = 0.
В первом случае для альтернативы aj, учитывая, что
c ∈ aj, имеем
Во втором случае для этой же альтернативы получим
| Σ |
f(h) ≥ f(sj) + f(c) = 2, |
| h ∈ aj | |
так как c ∈ aj. Следовательно
F(R1) ⊂ {fc | c ∈ C}. 
Окончательный ответ о принципиальной возможности решения
обратной задачи дает
Теорема 2.7
K(R) = K0, где
R = (S, C, A1 ∪ {a0}),
a0 = <c ∈ C | c(S) ∈ K0>.
Доказательство. По определению класса распознавания
K(R) = {f(S) | f ∈ F(R)}.
Множество F(R) составляют функции из F(R1), дополнительно
удовлетворяющие альтернативе a0. В соответствии с леммой 2.6,
элементы F(R1) есть функции вида fc, для которых fc(c) = 1.
Учитывая, что a0 ⊂ C, имеем:
F(R) = {fc | c ∈ a0}.
Отсюда:
K(R) = {fc(S) | c ∈ a0}.
По определению функции fc имеем:
K(R) = {c(S) | c ∈ a0}.
Из определения альтернативы a0 окончательно следует:
K(R) = {c(S) | c(S) ∈ K0} = K0. 
Пример.
Пусть k = 3, S = {s1,s2,s3},
K0 = {{s1},{s2},
{s3},{s1,s2},
{s2,s3},
{s1,s2,s3}}.
Используя порядок на множестве основных фактов, каждую
характеристическую функцию можно представить строкой в алфавите {0,1}.
C = <000,001,010,011,100,101,110,111>,
a1 = <s1, 000,001,010,011>,
a2 = <s2, 000,001,100,101>,
a3 = <s3, 000,010,100,110>.
В качестве искомой ПА-системы теорема 2.7 предлагает рассматривать
(S,C,{C,a0,a1,a2,a3}),
где a0 = <100,010,001,110,011,111>. 
Замечание 2.8
Поскольку a0 ⊂ C, то ПА-систему R из теоремы 2.7 можно
упростить следующим образом: (S, a0, {a0,a'1, ..., a'k}), где
a'i = ai \ (C \ a0) (i=1,..,k). 
Итак, выразительные возможности простых систем альтернатив
являются достаточно богатыми - они позволяют, по крайней мере
теоретически, формировать любой класс распознавания.
2.2 Логический вывод в системах альтернатив
Допустим, что класс распознавания некоторой простой системы
альтернатив образуют всевозможные примеры решений задач из
проблемной области. Кроме того, считается известным некоторый
фрагмент одного из примеров. Требуется - посредством логического
вывода - установить (насколько это возможно) недостающие факты
этого примера. Напомним, что ситуации такого рода характерны для
задач распознавания. В первом приближении логический вывод в
системах альтернатив представляет собой задачу реконструкции
частично определенной функции из класса F(R):

Перейдем к подробному анализу задачи логического вывода.
Пусть R = (S,C,A) - некоторая ПА-система и L+ и L- -
подмножества фактов из H. Прежде всего нас будет интересовать
следующее множество.
Определение 2.9
Q(R,L+,L-) = {q ∈ Q(R) _ L+ ⊂ q, L- ∪ q = ∅}. 
Подмножество Q(R,L+,L-) образуют элементы из Q(R),
подтверждающие факты из L+ и опровергающие факты из L-.
Соглашение.
В связи с тем, что запись "Q(R,L+,L-)" используется
достаточно часто, будем использовать ее краткий эквивалент "QL". 
Для заданного множества QL определим два множества фактов.
Определение 2.10
| H+ = |
∪ |
q, |
|
H- = |
∪ |
(H \ q). |
|
q ∩ QL |
|
|
|
q ∩ QL |
|
Факты из H+ будем называть установленными,
факты из H+ - опровергнутыми. 
Установленные факты являются общими для всех элементов QL,
в частности, L+ ⊂ H+. Множество H- образуют все факты, которые
ни разу не встречаются в QL; очевидно, что L- ⊂ H-.
Задача 2.11 (Задача логического вывода)
Дано. ПА-система R = (S,C,A) и два непересекающихся
подмножества L+ и L- из S.
Требуется. Проверить условие QL = ∅, и, в случае QL ≠ ∅,
найти подмножества фактов
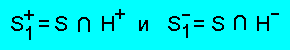

Рассмотрим два подхода к решению поставленной задачи.
Первый из них дает исчерпывающее и точное решение, однако,
представляет интерес только с теоретической точки зрения. Второй
способ, в некотором смысле, является менее точным, но более плодотворным.
Метод. (Полное решение задачи логического вывода)
| Этап 1. |
По известной ПА-системе R = (S,C,A) решить задачу 2.4 и
построить множество Q(R). |
| Этап 2. |
Используя определение 2.9, построить множество QL.
Если QL = ∅, то закончить вычисления с сообщением
"Выход за пределы класса распознавания". В противном
случае перейти к этапу 3. |
| Этап 3. |
Используя определение 2.10, построить множества
H+ и H-. |
| Этап 4. |
Построить искомые множества
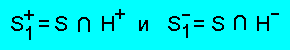 |
⌫
Таким образом, полное решение задачи логического вывода
предполагает решение системы булевых целочисленных уравнений (этап 1).
Рассмотрим второй (основной) подход к решению поставленной
задачи логического вывода.
Метод 2.12 (Процедура логического вывода)
Выполнить присваивания U+ = L+ и U- = L-.
Применить к системе альтернатив (в произвольном порядке)
следующие четыре правила вывода/преобразования.
Правило 2.12(1)
|
<..., hk-1, hk, hk+1, ...> ∈ A
|
|
hk ∈ U-
|
|
|
<..., hk-1, hk+1, ...> ∈ A
|
Правило 2.12(2)
|
<h1, ..., hk-1, hk, hk+1, ..., hm> ∈ A
|
|
hk ∈ U+
|
|
|
{h1, ..., hk-1, hk+1, ..., hm} ⊂ U-
|
Правило 2.12(3)
Правило 2.12(4)
Метод заканчивает свою работу либо в результате применения правила 2.12(4),
либо тогда, когда первые три правила не приносят более новой информации о
множествах A, U+ и U-.
В последнем случае решением задачи является множества
S+ = S ∪ U+ и
S- = S ∪ U-. 
Результат работы процедуры логического вывода не зависит от
порядка применения правил. Дело в том, что каждое из этих правил
представляет собой частный прием выявления значений неизвестных
в системе булевых уравнений вида
f(h1) + ... + f(hk-1) + f(hk) + f(hk+1) + ... + f(hm) + 0 = 1
Правило 2.12(1) утверждает, что если для некоторого уравнения
f(hk) = 0, то это уравнение можно переписать в виде
f(h1) + ... + f(hk-1) + f(hk+1) + ... + f(hm) + 0 = 1
Правило 2.12(2) утверждает, что если для некоторого уравнения
f(hk) = 1, то f(hi) = 0 (i=1,...,k-1,k+1,...,m).
Правило 2.12(3) утверждает, что если некоторое уравнение
имеет вид f(h) + 0 = 1 (т.е. m = 1), то f(h) = 1.
Правило 2.12(4) утверждает, что наличие в системе уравнения 0 = 1
(т.е. m = 0) означает, что система уравнений не имеет решения.
Учитывая приведенную интерпретацию правил, примем следующее
Соглашение.
Будем считать, что правило 2.12(1) выполняет замену альтернативы:
A = (A \ {a}) ∪ {a \ {hk}},
где a =<..., hk-1, hk, hk+1, ...>. 
При таком подходе побочным результатом работы процедуры
логического вывода будет модифицированное множество A, которое
называется остаточной системой альтернатив.
Пример.
Рассмотрим ПА-систему R = (S,C,A), где S = {i,j,k,m,n},
C = {x,y,z} и A = {, , , }. Приведем
возможную трассу процедуры логического вывода для случая
L+ = {i}, L- = ∅.
Применяемое правило.
Альтернатива [и факт]. |
(Остаточная) система альтернатив |
U+ |
U- |
| 1 |
2 |
3 |
4 |
|
<i,x,y> |
<j,x> |
<j,k,y> |
<m,n,y,z> |
i |
|
| 2.12(2) 1 и i |
|
<i> |
<j,x> |
<j,k,y> |
<m,n,y,z> |
i |
x y |
| 2.12(1) 2 и x |
|
<i> |
<j> |
<j,k,y> |
<m,n,y,z> |
i |
x y |
| 2.12(3) 2 |
|
<i> |
<j> |
<j,k,y> |
<m,n,y,z> |
i j |
x y |
| 2.12(2) 3 и j |
|
<i> |
<j> |
<j> |
<m,n,y,z> |
i j |
x y k |
| 2.12(1) 4 и y |
|
<i> |
<j> |
<j> |
<m,n, ,z> |
i j |
x y k |
| Конец. |
Результаты вывода:
S+ = S ∪ U+ = { i, j } и
S- = S ∪ U- = { k }.
Остаточная система альтернатив имеет вид:
<i>, <j>, <m,n,z>. 
В рассмотренном примере U+ = H+
и U- = H-, однако так бывает не всегда. В случае
непротиворечивого вывода (QL ≠ ∅) имеют место соотношения
U+ ⊂ H+, U- ⊂ H-
и, соответственно,
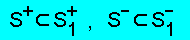 Таким образом, используя множества U+ и U- в
качестве приближений для H+ и H-, приходится считаться
с тем, что процедура логического вывода не во всех ситуациях дает
исчерпывающее решение задачи 2.11. В дальнейшем будет показано,
что эвристический характер процедуры не сказывается на
использовании наиболее употребительных формул логики высказываний.
Таким образом, используя множества U+ и U- в
качестве приближений для H+ и H-, приходится считаться
с тем, что процедура логического вывода не во всех ситуациях дает
исчерпывающее решение задачи 2.11. В дальнейшем будет показано,
что эвристический характер процедуры не сказывается на
использовании наиболее употребительных формул логики высказываний.
Замечание.
Результатом работы процедуры логического вывода наряду с множествами
S+ и S- можно считать множества U+ и
U-. 
Правила 2.12(2) и 2.12(3) позволяют расширять множества U+
и U-. Они являются простейшими образцами для распознавания
состояний остаточной системы альтернатив. В конкретных
реализациях мощность процедуры логического вывода может быть
увеличена за счет добавления более изощренных образцов.
Правило 2.12(4) позволяет в некоторых случаях установить
равенство QL = ∅, что означает наличие противоречий в исходной
системе альтернатив и заданных множествах L+ и L-. Однако,
возможны такие конструкции альтернатив, для которых правило
2.12(4) не способно выявить равенство QL = ∅.
Например, если остаточная система содержит изолированные альтернативы
<h1, h2>
<h3, h4>
<h5, h6>
<h1, h3, h5>
<h2, h4, h6>,
то QL = ∅, но процедура логического вывода не сможет установить
этот факт и, вполне вероятно, выдаст в качестве результата
некоторые множества U+ и U-.
Последнее обстоятельство является весьма неприятным с
теоретической точки зрения, но вполне приемлемым для
практической реализации баз знаний в виде систем альтернатив.
Необходимо только гарантировать, что и в ходе формирования базы
и при ее эксплуатации будет использоваться одна и та же
процедура логического вывода.
Подчеркнем, что процедура логического вывода является
составной частью аппарата альтернатив и сознательное
использование особенностей этой процедуры позволяет
рассматривать не только статические характеристики ПА-систем, но
и их динамические, функциональные свойства.
2.3. Модули знаний в системах альтернатив
Рассмотрим абстрактную ситуацию конструирования в виде
системы альтернатив заранее известной базы знаний. Исходным
материалом является множество основных фактов, выбранных для
описания проблемной области. На каждом шаге построения
разработчик базы выбирает некоторое (вообще говоря, весьма
ограниченное) подмножество фактов Si и связывает их в
определенной функциональной зависимости, т.е. фактически создает
мини-систему альтернатив Ri= (Si, Ci, Ai). В дальнейшем такие
системы будем называть модулями знаний. В конечном итоге, база
знаний, содержащая n модулей, может быть представлена
ПА-системой R = (S, C, A), в которой
S = S1 ∪ ... ∪ Sn,
C = C1 ∪ ... ∪ Cn,
A = A1 ∪ ... ∪ An.
Формально, такой метод построения баз знаний основывается
на следующем утверждении.
Лемма 2.13
Для любого модуля Ri имеет место вложение
{ D ∩ Si | D ∈ K(R) } ⊂ K(Ri).
Доказательство. Пусть D - произвольный элемент K(R), и Ri -
некоторый модуль. Покажем, что D ∩ Si ∈ K(Ri).
Поскольку D ∈ K(R), то в классе F(R) существует функция f
такая, что f(S) = D. Функция f удовлетворяет ПА-системе R и, в
частности, удовлетворяет всем альтернативам Ai. Обозначим fi
функцию, полученную из f сужением ее области определения S ∪ C
до множества Si ∪ Ci.
Функция fi сохраняет все свойства f по
отношению к альтернативам Ai.
Следовательно, fi удовлетворяет
модулю Ri, т.е. fi(Si) ∈ K(Ri).
Для множества fi(Si) имеем
fi(Si) =
{ s ∈ Si | fi(s) = 1 } =
{ s ∈ Si | f(s) = 1 } =
{ s ∈ S | f(s) = 1} ∩ Si =
D ∩ Si. 
При построении базы знаний, во всяком случае, на этапе ее
первоначального составления, принимается гипотеза о том, что все
модули являются независимыми и в процессе логического вывода
могут соединяться в произвольные цепочки причинно-следственных
связей для достижения поставленных целей. Применительно к
системам альтернатив гипотеза о независимости состоит в том, что
для любой пары модулей Ri и Rj (i ≠ j) имеет место равенство
Ci ∩ Cj = ∅. Т.е. каждый модуль имеет свое собственное множество
вспомогательных фактов. Конечно, в реальных системах гипотезу о
независимости модулей приходится ослаблять, вместе с тем возможности
ослабления обусловливаются спецификой представления модулей.
Ранее была доказана теорема 2.7, согласно которой
разработчик базы знаний может построить модуль с произвольным
классом распознавания. Доказательство содержит универсальный
метод построения модулей, но этот метод является неэффективным,
поскольку согласно замечанию 2.8 предполагает построение ||K(R)||
вспомогательных утверждений. Рассмотрим некоторые конструкции
модулей, представляющие интерес с практической точки зрения.
2.3.1. Модуль альтернативы
Прежде всего необходимо отметить, что саму альтернативу
< s1, ..., sm >
можно рассматривать в качестве модуля Ra, связывающего взаимоисключающие
факты из множества S = { s1, ..., sm }.
Очевидно K(Ra) = { {s1}, ..., {sm} }.
В ходе выполнения процедуры логического вывода модуль может
функционировать двумя способами.
1).Если si ∈ L+ для некоторого si из S, то S \ {si} ⊂ U-.
2).Если S \ {si} ⊂ L- для некоторого si из S, то si ∈ U+.
Схематично оба вида функционирования для случая, скажем,
m = 3 и i = 2 могут быть представлены следующими диаграммами:
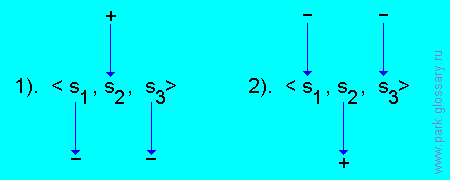
Приведенные схемы функционирования справедливы также и для
альтернатив, содержащих вспомогательные факты.
Замечание.
Если факты s1, ..., sm рассматривать как высказывания,
тогда класс распознавания альтернативы < s1, ..., sm >
можно рассматривать как множество всех интерпретаций, при которых
истинна некоторая правильно построенная формула Ф. Упомянутое
множество интерпретаций содержит ровно m наборов:
| s1 |
s2 |
s3 ... |
sm |
| И | Л | Л ... | Л |
| Л | И | Л ... | Л |
| Л | Л | И ... | Л |
| ... |
| Л | Л | Л ... | И |
С использованием традиционных для логики высказываний [49] связок
{ ¬, И, ИЛИ } формула Ф может быть представлена весьма сложной ДНФ:
s1 И ¬s2 И ... И ¬sm
ИЛИ
¬s1 И s2 И ... И ¬sm
ИЛИ
...
ИЛИ
¬s1 И ¬s2 И ... И sm 
Легко показать, что в случае m > 2 не существует бинарной,
ассоциативной и коммутативной операции * такой, что
Ф = s1 * ... * sm
Для m = 2 такой связкой является разделяющее или. 
Замечание.
Интересно отметить, что любую альтернативу
< h1, ..., hm >,
содержащую более трех фактов (m > 3) можно представить в виде
эквивалентного модуля знаний:
< h1,h2,c2 >
< c2,h3,c3 >
...
< cm-3,hm-2,cm-2 >
< cm-2,hm-1,hm >,
где c2, ..., cm-2 - вспомогательные факты модуля. В этом модуле
все альтернативы содержат ровно три факта. 
Замечание 2.14
Если s - некоторый факт и < s,h > ∈ A, то факт h можно
рассматривать, как ¬s. То есть:
Если s ∈ L+, то h ∈ U-;
Если s ∈ L-, то h ∈ U+. 
2.3.2. Модуль несовместимости
Модулем несовместимости Rн для фактов s1, ..., sm
называется альтернатива
< s1, ..., sm, c >,
где c - вспомогательный факт.
K(Rн) = { ∅, {s1}, ..., {sm} }.
В отличии от альтернативы, для модуля несовместимости
возможен только первый вид функционирования.
В дальнейшем изложении модуль несовместимости играет двоякую роль. С одной
стороны, он позволяет задавать в базе знаний неполные ряды несовместимых
фактов, а с другой - используется в качестве обозначения.
Соглашение.
Запись [ h1, ..., hm ] будем понимать как краткий
эквивалент альтернативы < h1, ..., hm, c>
с уникальным вспомогательным фактом c. 
2.3.3. Модуль запрета
Модулем запрета [13] Rз для фактов S = { s1 , ..., sm }
называется ПА-система
[ s1, c1 ]
...
[ sm, cm ]
< c1, ..., cm >
Класс распознавания этого модуля содержит все подмножества
основных фактов, кроме самого S.
K(Rз) = 2S \ {S}.
Доказательство. Предположим, что S ∈ K(Rз), тогда
существует функция f ∈ F(Rз), для которой f(S) = S.
Рассмотрим свойства этой функции. Из альтернативы
[ si, ci ] (i = 1, ..., m)
следует, что f(ci) = 0. >Следовательно,
для альтернативы
< с1, ..., cm > имеем:
f(c1) + ... + f(cm) = 0,
то есть f ∉ F(Rз),
а значит S ∉ K(Rз).
Рассмотрим произвольное подмножество S' из S такое, что
S \ S' ≠ ∅. Не ограничивая общности, можно считать,
что S' = {s1, ..., sk}, где k < m.
Определим функцию fm следующим образом:
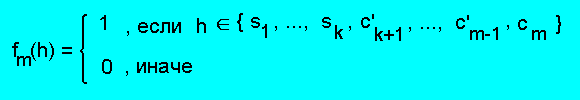 где ci - уникальный вспомогательный факт для альтернативы
[ si, ci ]. По построению функция fm
удовлетворяет ПА-системе Rз. Поэтому S' ∈ K(Rз).
где ci - уникальный вспомогательный факт для альтернативы
[ si, ci ]. По построению функция fm
удовлетворяет ПА-системе Rз. Поэтому S' ∈ K(Rз).

Модуль позволяет опровергать один факт при наличии всех
остальных. Другими словами, если S \ {s} ⊂ L+ для некоторого s,
то s ∈ U-.
Пример, m = 3, L+ = {s1, s3}.
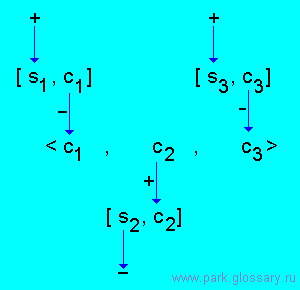 
Соглашение.
Для сокращения записи модуль запрета для фактов
s1, ..., sm будем обозначать
ЗАПРЕТ(s1, ..., sm). 
Замечание.
Если факты s1, ..., sm рассматривать как высказывания,
тогда ЗАПРЕТ(s1, ..., sm) представляет собой утверждение
¬s1 ИЛИ ... ИЛИ ¬sm.
Учитывая замечание 2.14, с помощью модуля запрета можно построить любую
элементарную дизъюнкцию. В частности, система альтернатив
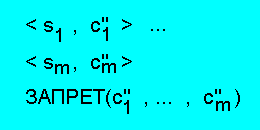 реализует утверждение
s1 ИЛИ ... ИЛИ sm.
реализует утверждение
s1 ИЛИ ... ИЛИ sm. 
Замечание.
Для m = 2 модули [ s1, s2 ] и
ЗАПРЕТ(s1, s2) эквивалентны друг другу. 
2.3.4. Модуль импликации
Модулем импликации Rи для фактов
S = {s0, s1, ..., sm } называется ПА-система
[ s1, c1 ]
...
[ sm, cm ]
< s0, c1, ..., cm >.
Рассмотрим класс распознавания модуля импликации.
K(Rи) = K+ ∪ K-, где
K+ = {D ∈ K(Rи) | s0 ∈ D},
K- = {D ∈ K(Rи) | s0 ∉ D}.
Множеству K+ соответствует остаточная система альтернатив,
полученная из Rи при L+ = {s0} и L- = ∅.
Эта система имеет вид:
< s0 >, [ s1 ], ..., [ sm ],
т.е. допускает любые подмножества из
S' = { s1, ..., sm }. Следовательно,
K+ = {D ∪ {s0} | D ⊂ S'}.
Аналогично, множеству K-соответствует остаточная система
альтернатив
[ s1, c1 ], ...,
[ sm, cm ],
< c1, ..., cm >,
полученная из Rи при L+ = ∅ и L- = {s0}.
Остаточная система представляет собой ЗАПРЕТ(s1, ..., sm), поэтому
K- = 2S' \ {S'}. 
Таким образом, имеем
K(Rи) = K+ ∪ (2S' \ {S'}) = (K+ ∪ 2S') \ {S'} = 2S \ {S'}.
Класс распознавания модуля импликации содержит все подмножества
основных фактов, за исключением S'. 
ПА-система Rи в ходе выполнения процедуры логического
вывода может функционировать двумя способами.
1). Если S' ⊂ L+, то s0 ∈ U+.
Например, m = 2, L+ = {s1, s2}.
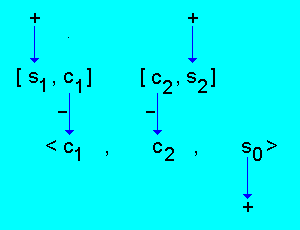
2). Если s0 ∈ L- и S' \ {s} ⊂ L+ для некоторого s ∈ S', то s ∈ U-.
Например, m = 3, L+ = {s1, s2}, L- = {s0}.
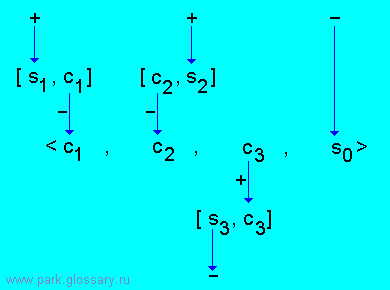
Первый вид функционирования соответствует правилу "ЕСЛИ s1
и ... и sm, ТО s0". Второй вид реализует возможность рассуждений
"от противного".
2.3.5. Модуль продукции
Продукцией для фактов S = { s0, s1, ..., sm }
называется ПА-система Rп:
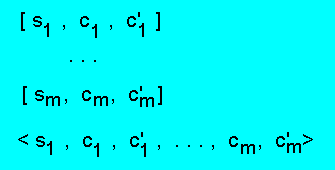
Легко убедиться, что K(Rп) = K(Rи), однако, в отличии от
модуля импликации, для продукций возможен только первый тип функционирования.
Пример m = 3, L+ = { s1, s2},
L- = { s0 }. В этом случае процедура логического вывода
строит остаточную систему альтернатив
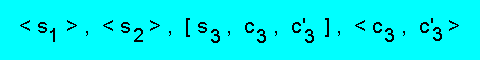 Правила анализа остаточной системы 2.12(1) и 2.12(2) не позволяют опровергнуть
факт s3 и присоединить его к U-. Заметим однако, что
если s3 будет установлен средствами некоторого другого модуля, то
процедура логического вывода немедленно обнаружит выход за
пределы класса распознавания.
Правила анализа остаточной системы 2.12(1) и 2.12(2) не позволяют опровергнуть
факт s3 и присоединить его к U-. Заметим однако, что
если s3 будет установлен средствами некоторого другого модуля, то
процедура логического вывода немедленно обнаружит выход за
пределы класса распознавания.
2.3.6 Структурирование систем альтернатив
В современных системаx искусственного интеллекта модули
знаний представляют не единым "мешком", а структурой автономных
фрагментов, подключающихся к работе в зависимости от тех или
иных условий. С этой точки зрения представляют интерес
возможности структурирования ПА-систем.
Свяжем с некоторым модулем знаний R = (S,C,A) факт sR. Будем
говорить, что модуль R является необязательным, если его альтернативы не
участвуют в выводе до тех пор, пока sR ∉ U+.
Факт sR называется флагом существования модуля R.
Покажем, что средствами аппарата альтернатив можно представлять
необязательные модули знаний. Прежде всего, рассмотрим модуль R=
следующего вида:
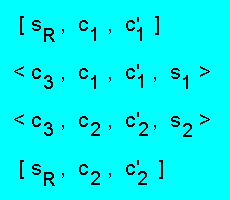
Непосредственной проверкой легко убедиться, что
K(R=) = { {sR}, {sR,s1,s2},
∅, {s1}, {s2}, {s1,s2} }
Рассмотрим функциональные характеристики этого модуля.
Если sR ∈ U+,
то {c1,c2} ⊂ U-
и остаточная система имеет вид:
< c3, s1 >, < c3,s2 >,
что гарантирует следующее поведение: s1 ∈ U+
(s1 ∈ U-)
тогда и только тогда, когда
s2 ∈ U+ (s2 ∈ U-). Если
sR ∈ U-,
то, как следует из состава класса распознавания, факты
s1 и s2 независимы друг от друга.
Итак, только при установленном флаге существования факты
s1 и s2 проявляют себя одинаково
в ходе логического вывода.
Введем для альтернатив ПА-системы R= следующее обозначение:
eq(s1,s2 | sR).
Рассмотрим теперь произвольный модуль R = (S,C,A) и факт
sR, sR ∉ S, который должен выступать в роли флага существования
модуля R. Построим необязательный модуль знания R' следующим образом:
R' = (S ∪ { sR }, C ∪ CS, A'),
где СS = {s' | s ∈ S},
A' = { eq(s,s' | sR) | s ∈ S} ∪ AS,
множество AS получается из A посредством замены всех вхождений
фактов s из S на факты s' из CS. Свойства модуля R=
гарантируют, что альтернативы из AS не будут участвовать в
логическом выводе, пока не будет установлен флаг sR.
Пример.
Необязательный модуль альтернативы
< s1, s2, s3 > имеет вид:
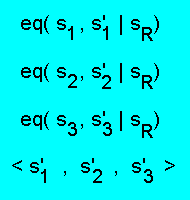

Таким образом, аппарат альтернатив, по-крайней мере,
теоретически позволяет представлять необязательные модули
знаний, что позволяет структурировать систему альтернатив.
2.4. Реализация процедуры логического вывода
Прежде чем привести функциональную схему процедуры
логического вывода вывода, примем соглашения, каждое из которых
может быть проверено или вычислено один раз на подготовительном этапе.
Соглашение.
| (1) |
Будем предполагать, что в системе альтернатив изначально
отсутствуют пустые альтернативы и альтернативы, содержащие
ровно один факт. |
| (2) |
Будем предполагать, что для каждого факта h из H
известно множество альтернатив A(h), использующих h:
A(h) = {a ∈ A | h ∈ a}. |

Принятые соглашения позволяют рассматривать правила 2.12(3) и 2.12(4) как
процедуры анализа альтернативы, полученной в результате применения правила
2.12(1).
Работу машины вывода определяют четыре основные процедуры:
— FIX(h : факт);
— REF(h : факт);
— EXTFIX(h : факт; var a : альтернатива);
— EXTREF(h : факт; var a : альтернатива).
В данном случае для описания процедур используется нотация
языка ПАСКАЛЬ. При определении процедур термин "активизировать"
будем понимать как аналог команды FORK [50], которая инициирует
развитие нового независимого процесса вычислений соответствующей
процедуры.
Процедура FIX.
Если h ∈ U+, то
(1) квалифицировать факт h как установленный: U+ = U+ ∪ {h};
(2) для всех альтернатив a из A(h) активизировать EXTFIX(h,a). 
Процедура REF.
Если h ∈ U-, то
(1) квалифицировать факт h как опровергнутый: U- = U- ∪ {h};
(2) для всех альтернатив a из A(h) активизировать EXTREF(h,a). 
Процедура EXTFIX.
(1) уничтожить в A альтернативу a: A = A \ {a}.
(2) реализовать правило 2.12(2) с альтернативой a и фактом h:
для всех фактов h' (h' ≠ h и h' ∈ a) активизировать REF(h'). 
Процедура EXTREF.
| (1) |
| уничтожить в A альтернативу a:
| A = A \ { a }; |
| уничтожить в a факт h:
| a = a \ { h }; |
| произвести замену альтернативы:
| A = A ∪ { a }. |
|
| (2) |
анализировать состояние остаточной альтернативы a:
Правило 2.12(4).
Если a = < >, то СТОП("Выход за пределы класса распознавания");
Правило 2.12(3).
Если a = < h' >, то активизировать FIX(h'). 
|
При запуске алгоритма логического вывода активизируются процедуры FIX(h)
для h ∈ L+ и REF(h) для h ∈ L-.
Все активизированные процедуры могут выполняться в любом
порядке, независимо друг от друга, что позволяет естественным
образом распараллеливать работу процедуры логического вывода.
Отметим, что в системе ФИАКР машина вывода реализована на
однопроцессорной ЭВМ, при этом активизированные процедуры
заносятся в так называемую очередь процессов и обрабатываются
последовательно. Очередь организована таким образом, чтобы
сократить количество обращений к памяти на внешних носителях,
где, собственно, и хранится система альтернатив.
С целью формирования трассы причинно-следственных связей,
возникающих в ходе логического вывода, процедуры FIX и REF
дополняются еще одним параметром - указателем на альтернативу, в
которой данный факт был установлен или опровергнут. Для исходных фактов из
L+ и L- используется специальное значение указателя.
Другими словами, для каждого факта из U+ ∪ U-
хранится указатель на альтернативу, объясняющую его текущее состояние.
Расшифровку и интерпретацию причинно-следственных связей осуществляет
подсистема объяснений.
Наибольшие затруднения при программной реализации процедуры
логического вывода вызывает применение правила 2.12(4),
поскольку действия, предписываемые этим правилом,
непосредственно в системах альтернатив не предусматриваются.
Проблема состоит в том, что при возникновении ситуации выхода за
пределы класса распознавания - в интересах подсистемы объяснений
- необходимо каким-то разумным способом остановить все
активизированные в настоящий момент процессы. В связи с этим
предлагается стандартная модификация системы альтернатив и
процедуры логического вывода, снимающая указанные затруднения.
2.5 Модифицированные системы альтернатив
Зафиксируем ПА-систему R = (S,C,A). Введем новый вспомогательный
факт t (t ∉ H) и связанное с ним множество T, T = { t }. По
системе R построим ПА-систему
R = ( S, C ∪ T, A ),
где A = { a ∪ T | a ∈ A }.
Если, например, система R состоит из альтернатив
< s1, c1, c2 >
< s2, c3, c4 >
< c1, c2, s3 >,
тогда систему R образуют альтернативы
< s1, c1, c2, t >
< s2, c3, c4, t >
< c1, c2, s3, t > .
Связь между системами R и R определяет следующая
Теорема 2.15
Q(R) = Q(R) ∪ { T }.
Доказательство. Множество F(R) можно разбить на два
непересекающиеся подмножества
F- = {f ∈ F(R) | f(t) = 0} и
F+ = {f ∈ F(R) | f(t) = 1}.
Множеству F- соответствует остаточная система альтернатив,
полученная из R при L+ = ∅ и L- = T.
По определению ПА-системы R остаточная система есть R.
Следовательно, подмножество F составляют функции класса F(R), доопределенные
значением 0 для факта t.
Поэтому { f() | f ∈ F- } = Q(R).
Рассмотрим произвольную функцию f из F+. В соответствии с
принятыми соглашениями, каждый факт h (h ≠ t) входит, по-крайней
мере, в одну альтернативу. Для этой альтернативы равенство из
определения 2.2 имеет вид
... + f(h) + f(t) = 1.
С учетом того, что f(t) = 1 имеем f(h) = 0.
Другими словами, подмножество F+ состоит из единственной функции
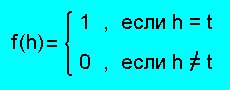
Окончательно имеем:
Q(R) =
{f(H) | f ∈ F-}
∪ {f(H) | f ∈ F+} =
Q(R) ∪ T. 
Следствие. K(R) = K(R) ∪ {∅}. 
Таким образом, указанное преобразование практически не
влияет на выразительную мощность исходной ПА-системы. Пустой
объект, появляющийся в классе распознавания, с практической
точки зрения абсолютно не реален, поскольку противоречит даже
исходной информации об объекте консультации - множеству L+ при
L+ ≠ ∅.
С модифицированной системой альтернатив связана особая
процедура логического вывода.
Метод 2.16
Выполнить присваивания: V - = L-, V+ = L+, V = ∅.
Применить к системе альтернатив R
(в произвольном порядке) следующие правила вывода/преобразования:
Правило 2.16(1)
|
< ..., hk-1, hk, hk+1, ..., t > ∈ A
|
|
hk ∈ V -
|
|
|
<..., hk-1, hk+1, ..., t > ∈ A
|
Правило 2.16(2)
|
< h1, ..., hk-1, hk, hk+1, ..., hm, t > ∈ A
|
|
hk ∈ V
|
|
|
{ h1, ..., hk-1, hk+1, ..., hm } ⊂ V -
|
Правило 2.16(2')
|
< h1, ..., hm, t > ∈ A
|
|
t ∈ V+
|
|
|
{ h1, ..., hm } ⊂ V -
|
Правило 2.16(3)
Правило 2.16(4)
Метод заканчивает работу, когда правила вывода не приносят
более новой информации о множествах V -, V, V+ и A.
Результатом работы метода являются множества
V -, V и V+. 
Правила вывода из метода 2.16 реализуют некоторые приемы
преобразования и решения системы булевых уравнений вида
f(h1) + ... + f(hk-1) + f(hk)
+ f(hk+1) + ... + f(hm) + f(t) = 1
Правила 2.16(3) и 2.16(4) фиксируют наличие в системе двух
частных случаев уравнений: f(h) + f(t) = 1 и f(t) = 1.
Правило 2.16(1) утверждает, что если для некоторого
уравнения f(hk) = 0, то это уравнение можно переписать в виде
f(h1) + ... f(hk-1) +
+ f(hk+1) + ... + f(hm) + f(t) = 1
Правило 2.16(2) утверждает, что наличие в системе уравнения
f(h1) + ... + f(hk-1) + f(hk) +
f(hk+1) + ... + f(hm) + f(t) = 1
и уравнения f(hk) + f(t) = 1, гарантирует
f(hi) = 0 (i≠ k).
Правило 2.16(2') утверждает, что если для некоторого
уравнения f(t) = 1, то f(hi) = 0 (i=1,...,m).
Факты из множества V \ L+, полученные с помощью правила
2.16(3), переходят в разряд установленных только в том случае,
когда опровергается факт t. Поэтому факты этого класса можно
считать установленными условно впредь до проверки равенства
QL = ∅.
Как отмечалось ранее, правила 2.12(1), 2.12(2), 2.12(3) и
2.12(4) не всегда способны проверить наиболее критичное для
логического вывода условие QL = ∅. Поэтому, с концептуальной
точки зрения, именно условный вывод в наибольшей степени
отвечает природе систем альтернатив. Можно считать, в
модифицированной системе R факт t есть символический эквивалент
условия QL = ∅ для ПА-системы R. Перед запуском процедуры вывода
t находится в неопределенном состоянии, то есть не принадлежит
ни одному из множеств V -, V и V+.
Правила вывода 2.16(1), 2.16(2) и 2.16(3) позволяют делать выводы в условиях
неопределенного факта t. Правило 2.16(4) позволяет установить t,
что соответствует выходу за пределы класса распознавания в
системе R, и, наконец, правило 2.16(2') непротиворечивым образом
доопределяет действия процедуры вывода в этом случае.
Соотношение между методами 2.12 и 2.16 определяет следующая
Теорема 2.17
Пусть R = (S,C,A) - ПА-система. Для любых подмножеств L+ и
L- из H, удовлетворяющих условию QL ≠ ∅, имеют место равенства
V = U+, V - = U- и V+ = ∅.
Доказательство. Для упрощения последующих выкладок введем обозначение:
Q = Q(R,L-,L+).
Доказательство теоремы проведем в два этапа.
Сначала докажем, что t ∉ V+.
Предположим обратное: t ∈ V+. Тогда в соответствии с
правилом 2.16(2') Q = {T}. С другой стороны имеем:
Q = { q ∈ Q | t ∉ q } ∪ { q ∈ Q | t ∈ q }.
Рассмотрим первое из этих подмножеств
{q ∈ Q | t ∉ q} = Q(R,L+, L- ∪ T) = Q(R,L+,L-).
Следовательно,
QL ⊂ Q или QL ⊂ {T},
что противоречит условию теоремы, поскольку t ∉ Q по определению системы
R.
Перейдем ко второму этапу доказательства. Так как t ∉ V+,
то при построении множеств V+, V- и V использовались только
правила 2.16(1), 2.16(2) и 2.16(3). Непосредственно из условия
теоремы вытекает, что при построении множеств U+ и
U- использовались правила 2.12(1), 2.12(2) и 2.12(3).
В системе R и правилах 2.16(1), 2.16(2) и 2.16(3)
произведем следующие преобразования альтернатив: a = a \ T.
Полученная таким образом ПА-система R1 совпадает с системой R.
Соответственно, правила 2.16(1), 2.16(2) и 2.16(3)
трансформируются в правила 2.12(1), 2.12(2) и 2.12(3) с
точностью до переименования множеств V и V -
во множества U+ и U-. 
Таким образом, переход от системы альтернатив R (с процедурой вывода 2.12)
к системе R (с процедурой вывода 2.16)
не влияет на мощность логического вывода. Кроме того, все
правила из 2.16 реализуются в терминах систем альтернатив, что
упрощает программирование машины вывода.
С точки зрения практической реализации совсем не обязательно
переходить от исходной ПА-системы R к модифицированной системе
R. Того же результата можно добиться,
модифицируя лишь правила вывода 2.16.
Метод 2.18 (Условный логический вывод)
Выполнить присваивания: V - = L-, V+ = L+, V = ∅.
Применить к системе альтернатив R (в произвольном порядке)
следующие правила вывода/преобразования:
Правило 2.18(1)
|
< ..., hk-1, hk, hk+1, ... > ∈ A
|
|
hk ∈ V -
|
|
|
<..., hk-1, hk+1, ... > ∈ A
|
Правило 2.18(2)
|
< h1, ..., hk-1, hk, hk+1, ..., hm > ∈ A
|
|
hk ∈ V
|
|
|
{ h1, ..., hk-1, hk+1, ..., hm } ⊂ V -
|
Правило 2.18(2')
|
< h1, ..., hm > ∈ A
|
|
t ∈ V+
|
|
|
{ h1, ..., hm } ⊂ V -
|
Правило 2.18(3)
Правило 2.18(4)
Метод заканчивает работу, когда правила вывода не приносят более новой
информации о множествах V+, V -, V и A.
Если V ≠ ∅, то результатом работы метода являются множества
S+ = S ∪ V и S= S ∪ V -. 
Формальный аппарат простых систем альтернатив используется:
— в инструментальной экспертной системе ФИАКР (глава III)
в качестве метода реализации баз знаний;
— в эвристическом методе восстановления контекстно-свободных
языков (п. 4.4.3) для выбора однотипных структур;
— в блоках анализа протоколов АСИЗ (п. 6.2.2) для построения
согласованных интерпретаций.
|