ВВЕДЕНИЕ

С каждым днем растет количество сайтов в сети Интернет. Профессия сайтостроителя (веб-дизайнера) становится весьма востребованной [1]. Параллельно растет спрос на программные инструменты, хотя бы частично облегчающие труд веб-дизайнера. По-настоящему, отрасль программирования для нужд веб-дизайна только-только зарождается, однако уже сейчас можно выделить одно противоречие, которое серьезно скажется на развитии отрасли. С одной стороны, веб-дизайнер по сути своего труда должен создавать оригинальные и запоминающиеся веб-произведения. С другой стороны, многократное применение одних и тех же программных инструментов порождает однотипные по своему оформлению сайты.

В этой ситуации развитие отрасли скорее всего пойдет двумя параллельными путями. Во-первых, будут создаваться и развиваться дорогостоящие и многофункциональные АРМ-ы, покрывающие весь цикл разработки веб-сайтов. Во-вторых, будут создаваться относительно простые утилиты для формирования отдельных веб-страниц, тиражирующие однажды найденное решение. Настоящую работу следует воспринимать в контексте второго пути, она посвящена конкретному методу "Галерея", предназначенному для порождения веб-страниц, именуемых картами сайтов.

 

ПОСТАНОВКА ЗАДАЧИ

Карта сайта - веб-страница, основное содержание которой составляет множество навигационных ссылок веб-сайта, структурированное в соответствии с логикой сайта. Обычно карта сайта представляет в наглядном виде многоуровневое соподчинение веб-страниц.

Исходными данными для метода генерации карт "Галерея" служит топология связей между веб-страницами сайта, заданная в виде ориентированного графа <V, W, g>, где
V - множество вершин - суть - множество веб-страниц, каждой из которых приписаны печатное наименование name(m) и URL-адрес href(m),
W - множество ориентированных ребер вида (p,q),
g - выделенная вершина из V, именуемая главной вершиной и соответствующая главной веб-странице.

Результатом применения метода "Галерея" к графу является текст страницы-карты на языке HTML, отражающий топологию заданного графа.

Идея метода состоит в разбиении графа на отдельные подграфы, допускающие относительно простое представление в виде схем специального вида. Полученные схемы размещаются на результирующей веб-странице, причем их взаимное расположение представляет одну из возможных иерархий соподчинения, а остальные связи моделируются внутренними гиперссылками. В дальнейшем изложении:
- под картой сайта будем понимать результат, полученный методом "Галерея",
- количество элементов множества A будем обозначать ↓A↓,
- вершины, непосредственно связанные с выделенной вершиной m из V, разделим на два множества:
   Imp(m) = { p | (p,m) in W }  и  Exp(m) = { q | (m,q) in W }.

В описании метода выделим три части: о разбиении графа на подграфы, о представлении подграфов схемами и о построении карты по набору схем.

 

О РАЗБИЕНИИ ГРАФА НА ПОДГРАФЫ

Метод "Галерея" основан на построении покрытия заданного графа <V, W, g> древовидными подграфами
Branch(m) = <V(m), W(m), m>,  m in V, каждый из которых имеет наглядное представление и местоположение на карте.

Определим семейство подграфов { Branch(m) }.
1. Выделим в отдельный класс "транзитные неветвящиеся" и "конечные" вершины графа:
    Trans = { m in V - {g} | ↓Imp(m)↓ = 1  и  ↓Exp(m)↓ ≤ 1 }
2. Для каждой вершины m из V - Trans определим множество V(m) так
    (a) m in V(m),  и  Exp(m) subset V(m),
    (б) Если q in V(m),  и  q in Trans, то Exp(q) in V(m).
3. Для каждой вершины m из V - Trans определим множество W(m) так
    W(m) = { (p,q) in W | p in V(m),  q in V(m) }.

Очевидно, что для каждого графа <V,W,g> семейство { Branch(m) | m in V - Trans } строится единственным образом. Для иллюстрации метода введем сквозной

Пример. Branch(n) = <V(n), W(n), n>, где
V(n) = { n, n₁, n₂, n₃, n₄, n₅ }, причем Imp(n) = { p },

name(n) = Организмы,
name(n₁) = Животные,
name(n₂) = Наследственность,
name(n₃) = Растения,
name(n₄) = Древесина,
name(n₅) = Лесные материалы,
name(p) = Жизнь,

W(n) = { (n,n₁), (n,n₂), (n,n₃), (n₃,n₄), (n₄,n₅) }.

 

О ПРЕДСТАВЛЕНИИ ПОДГРАФОВ СХЕМАМИ

Метод "Галерея" предполагает, что каждый подграф Branch(m) = <V(m), W(m), m> оформляется в виде самостоятельной схемы, ограниченной рамкой и имеющей уникальную закладку-якорь, служащую для переходов между схемами в пределах карты сайта. На рис. 1 приводится схема для подграфа Branch(n).
 

Рис.1. Схема представления подграфа Branch(n)

На схемах:
-1- главная вершина подграфа m (n; Организмы) выделяется жирным шрифтом и служит гиперссылкой для перехода к веб-странице href(m);
-2- имена вершин из V(m) - Trans (n₁; Животные) выделяются курсивом и разрядкой, они являются внутренними гиперссылками и используют закладки-якоря;
-3- имена остальных вершин (Наследственность, Растения, Древесина и Лесные материалы) являются гиперссылками на соответствующие веб-страницы (href(n₂), href(n₃), href(n₄), href(n₅)).

Каждую схему можно условно разделить на левую и правую части. Воображаемая вертикальная граница между частями схемы примыкает слева к наименованию главной вершины подграфа. Узкая левая часть имеет стандартную ширину, у подграфа Branch(g) левая часть может вообще отсутствовать.
 

Рис.2. Правая и левая части схемы

Правая часть схемы реализуется в виде традиционной иерархии соподчинения, принятой, скажем, в описании структуры файлов:
- вертикальный отрезок-шина, символизирует главную вершину подграфа;
- ребра подграфа представлены горизонтальными отрезками.

Cверху вертикальный отрезок-шина ограничен наименованием главной вершины (Организмы), а снизу помечен первой буквой того же наименования (О). Считается, что таким образом пользователь осваивает аппарат меток, который существенно используется в левой части схемы.

Левая часть схемы для подграфа Branch(m) = <V(m), W(m), m> представляет в наглядном виде множество Imp(m). В этой части схемы размещается обобщенная вертикальная шина с метками вершин из Imp(m). Для схемы Branch(n) множество Imp(n) состоит из единственной вершины с меткой Жизнь, и левая часть схемы имеет одну метку Ж. В общем случае, меток может быть несколько, и тогда они размещаются одна под другой. Каждая метка является внутренней гиперссылкой на соответствующую схему карты сайта.

Представление подграфа в виде схемы реализует процедура Diagram(m), которая для заданной вершины m сначала строит подграф Branch(m), а затем формирует html-код

<table>

<!-- Внутренняя часть html-текста Diagram(m) -->

</table>

Рис.3. Базовый примитив

Для сайтов с высокой посещаемостью существенно, что при построении этого кода, не используются средства графики (теги <img src=...>); базовый примитив схемы, приведенный на рис.3, реализуется html-кодом:

<table><tr>

<td style="border-left:black 2px solid"><hr width=20></td>

<td>Наименование</td>

</tr></table>

 

О ПОСТРОЕНИИ КАРТЫ ИЗ НАБОРА СХЕМ

Основная нагрузка по формированию html-кода карты для заданного графа <V, W, g> приходится на рекурсивную процедуру FormMap, которая получает на входе вершину графа m и величину отступа от левого края Indent. В своей работе процедура FormMap:
-1- использует для модификации отступа целочисленную константу Step;
-2- формирует глобальный "стоп-лист" StopDots вершин графа, [более] не подлежащих выводу в виде схем;
-3- сопоставляет каждой обработанной вершине локальное множество вершин Sons(m), формируя таким образом иерархию соподчинения схем.

Считается, что процесс построения карты запускается из некоторого объемлющего модуля и состоит из двух операторов:

Положить StopDots равным Trans;

Выполнить FormMap(g,0).

В общем случае процедура FormMap(m : вершина; Indent : целое) выполняет следующие шаги:
Шаг 1. WriteWithIndent(Indent, Diagram(m)).
Шаг 2. Построить подграф Branch(m) = <V(m), W(m), m>.
Шаг 3. Положить Sons(m) равным V(m) - StopDots - {m}.
Шаг 4. Положить StopDots равным StopDots + V(m).
Шаг 5. Для каждой вершины x из Sons(m) выполнить FormMap(x, Indent + Step).

Вывод с отступом WriteWithIndent, заявленный на шаге 1, реализуется html-кодом:

<div style="padding-left: Indent">

<!-- Diagram(m) -->

</div>

С помощью отступов демонстрируется глубина вложенности подграфа, то есть расстояние от главной вершины g до подграфа. Визуальный эффект от использования отступов может быть существенно усилен за счет дополнительного связывания глубины вложенности c толщиной рамки, которая вычисляется по формуле Thick = MaxDepth - Indent / Step, где MaxDepth - максимальное расстояние от главной вершины, достигаемое в заданном графе. Соответствующий html-код имеет вид:

<div style="padding-left:Indent">

<table border="Thick">

<!-- Внутренняя часть html-текста Diagram(m) -->

</table>

</div>

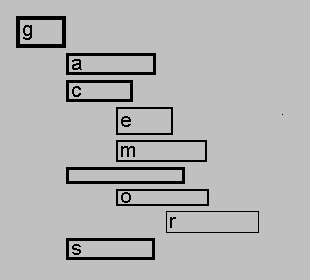Рис.4. "Лестница" схем>

Карта, полученная описанным алгоритмом, представляет собой формально построенную "лестницу" схем. Пример такой "лестницы" без детализации внутреннего содержимого схем приведен на русунке 4.

Структуры такого рода, содержащие 100 и более элементов, не удобны для пользователей. На случай большого количества вершин предлагается совмещать по горизонтали схемы вершин из множеств Sons(m). Такая модификация достигается за счет усложнения шагов 1 и 5.

Шаг. 1 (модифицированный).

Если  0 ≤ Indent,

то  WriteWithIndent(Indent, Diagram(m)),

иначе  Положить Indent равным -Indent.
Шаг. 5 (модифицированный).
5.1 Упорядочить, насколько это возможно, множество

Sons(m) = { x₁ .... x_k(m)},   k(m) = ↓Sons(m)↓, таким образом, что

Sons(x_н) = empty для вершин x_н с нечетными номерами, и

Sons(x_ч) ≠ empty для вершин x_ч с четными номерами.

5.2 Последовательно рассматривая вершины x_i из упорядоченного множества

Sons(m), действовать в соответствии со следующим правилом:

Если (i - нечетное) и (Sons(x_i) = пусто) и (i < k(m)),

то  5.2.1 Вывести с отступом Indent пару Diagram(x_i) и Diagram(x_i+1),

5.2.2 Положить i равным i + 1,

5.2.3 FormMap(x_i, - Indent - Step),

иначе  5.2.4 FormMap(x_i, + Indent + Step).

Модификация шага 1 позволяет без привлечения дополнительных параметров отменить вывод схемы для главной вершины подграфа, оставляя дальнейшие построения без изменений. Эта возможность используется на шаге 5.2.3.

Шаг 5.2.1 реализуется html-кодом:

<div style="padding-left: Indent">

<table border="0" cellpadding="0" cellspacing="0"><tr>

<td valign="top">

<!-- Diagram(x[i]) -->

</td>

<td valign="top" style="padding-left:16">

<!-- Diagram(x[i+1]) -->

</td>

</tr></table>

<div>

Здесь горизонтальный пробел между схемами для определенности установлен 16 px.

Применение модифицированной процедура FormMap для рассмотренного примера-лестницы порождает достаточно компактную карту, приведенную на рисунке 5.
 

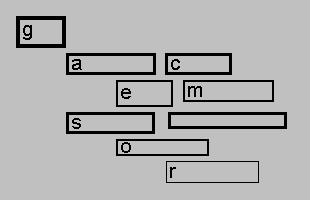Рис.5. "Галерея" схем

Важно отметить, что при таком "галерейном" методе размещения схем карта по-прежнему отражает структуру исходного графа, она понятна пользователям.

 

О ПРИМЕНЕНИИ МЕТОДА

Метод "Галерея" рассчитан на такие графы
-1- в которых каждая вершина достижима из главной по непрерывной цепочке ребер, и
-2- в которых относительно невелико множество фокусирующих вершин:

{ m in V - {g} | ↓Imp(m)↓ > 1 и ↓Exp(m)↓ ≤ 1 }, и

-3- которые "не слишком сильно" отличаются от деревьев:

для любого m из V - {g} имеет место ↓Imp(m)↓ in { 1, 2, 3}.

Практическое применение метода "Галерея" допускает варианты. Во-первых, метод можно включить в состав скрипта, каждый раз исполняемого на серверной стороне при получении запроса на карту сайта. Во-вторых, метод можно использовать только для построения статической карты. Второй вариант представляется предпочтительным, поскольку для вычисления параметра MaxDepth и выполнения шага 5.1 требуются дополнительные проходы, время и ресурсы.

 

ЗАКЛЮЧЕНИЕ

Метод "Галерея" применяется для формирования терминологической карты веб-ресурса www.glossary.ru - Служба тематических толковых словарей [2]. Станицами-вершинами служат крупные разделы, покрывающие терминологию отдельной науки или отдельного бизнеса. Опыт применения метода показывает, что он вполне пригоден для построения карт, связывающих несколько сотен веб-страниц.
 

ЛИТЕРАТУРА

1. Пауэлл Т. WEB-дизайн. - СПб.: БХВ-Петербург, 2005.
2. Мальковский М.Г., Соловьев С.Ю. Универсальное терминологическое пространство. Труды Международного семинара Диалог'2002 "Компьютерная лингвистика и интеллектуальные технологии", т.1. М.: Наука, 2002, с.266-270.

www.park.glossary.ru/serios/theory01.php

--------- * ---------

Точная ссылка: http://www.jip.ru/2008/24-29-2008.pdf:
Соловьев С.Ю. Об одном методе генерации страниц-карт для веб-сайтов. // Информационные процессы, www.jip.ru. Том 8, No.1, 2008, стр.24-39.

П|р|о|д|о|л|ж|е|н|и|е ►

Copyright ©
2000-2022
Web-and-Press