|
н а п р а в а х р е к л а м ы
|
|

|
Теория:
1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| 11
| 12
| 13
| 14
| 15
С.Ю.Соловьев
ОБРАЗНЫЕ ПРЕДСТАВЛЕНИЯ ТЕРМИНОЛОГИЧЕСКОЙ СЕТИ
Москва, 2008.
>>
Точная ссылка
- Введение
-
Стремление к наглядному представлению сложных явлений сродни самому процессу познания.
Представить → Увидеть → Доказать - вот типичная схема научного творчества.
Вовлечение компьютера в процесс представления уже давно [1] "подает большие надежды", однако исследования последних лет показали, что на самом деле компьютерная визуализация выдвигает новые задачи и нуждается в новых подходах.
В настоящей работе несколько необычно рассматривается известная задача визуализации локального фрагмента раскрашенного графа. Объектом исследования является УТП - универсальное терминологическое пространство [2] определений терминов научной и деловой лексики.
- Универсальное терминологическое пространство
-
Формально УТП можно рассматривать как граф
- вершинами которого являются электронные карточки с определениями терминов; а
- множество ориентированных ребер задается бинарными отношениями
это-есть(<Вершина>,<Понятийная-вершина>) или
относится-к(<Вершина>,<Понятийная-вершина>), где
- <Вершина> - в узком смысле - определение некоторого термина;
- <Вершина> - в широком смысле - понятие, заданное определением;
- <Понятийная вершина> - вершина графа, в которую входит хотя бы одно ребро;
- это-есть(A,B) - родовидовое отношение, в котором:
- B - родовое понятие для A; а
- A - подвид понятия B;
- относится-к(A,B) - бинарное отношение, в котором:
- B является областью применения для A; а
- A выступает аксессуаром для B;
содержательно A может быть частью, свойством или аспектом B,
A может так же выступать в качестве фигуранта в определении понятия B и т.д.
УТП - расширяющаяся структура, насчитывающая на начало 2008 года 37 выпусков, последний из которых имеет:
- 52225 вершин-определений, в том числе 7351 - понятийных;
- 70880 ребер-отношений, из которых:
- 33021 - связи "это-есть"; и
- 37859 - связи "относится-к".
Построение УТП - это редакторская работа, рассчитанная на использование интеллектуального потенциала человека, на его способность к обучению. Связи между вершинами-определениями устанавливаются научным редактором исходя из соотношений между понятиями.
Термин, определенный в некоторой вершине, служит также именем этой вершины. Кроме того, в УТП все понятийные вершины имеют дополнительные уникальные имена. Обычно дополнительное имя является производным от термина понятийной вершины. Например, термину "Программист" соответствует дополнительное имя "Программисты", термину "База данных" - дополнительное имя "Базы данных". Особый статус понятийных вершин связан с тем, что их контекст в УТП можно считать относительно законченным. По этой причине понятийные вершины рассматриваются как центры формирования специализированных глоссариев [3]. Собственно говоря, дополнительное имя понятийной вершины и есть заголовок глоссария.
- Фрагмент УТП
-
Введем классификацию вершин, находящихся в окрестности некоторой (понятийной) вершины t.
P(t) = { x | это-есть(t,x) } - родовые понятия для t;
S(t) = { x | это-есть(x,t) } - подвиды t;
A(t) = { x | относится-к(x,t) } - аксессуары t;
B(t) = { x | относится-к(t,x) } - области применения t;
BP(t) = B(t) + P(t) - область цитирования t;
AS(t) = A(t) + S(t) - состав понятия t;
L(t) = { x из BP(y) | для нек. y из AS(t) } \ {t} - смежные с t понятия, состав которых пересекается с составом t; альтернативно
L(t) = { x | AS(x) * AS(t) <> empty } \ {t};
s(t) = { x из S(t) | BP(x) = {t} } - собственные подвиды, не задействованные в других понятиях;
a(t) = { x из A(t) | BP(x) = {t} } - собственные аксессуары, не задействованные в других понятиях.
Соотношения между классами показаны на диаграмме (рисунок 1), разложенной для удобства восприятия на два слоя.
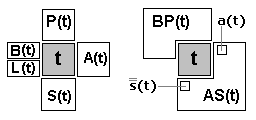 |
|
Рис.1. Диаграмма Эйлера-Венна |
Помимо ребер, непосредственно примыкающих к вершине t, в окрестности, вообще говоря, имеется некоторое количество ребер из УТП, соединяющих вершины AS(t) с вершинами из L(t).
Эти ребра с точностью до типов связей образуют множество W(t).
Обозначим k(w) - количество ребер вида (w,x) из W(t).
Очевидно, что для w из a(t) + s(t), имеет место k(w) = 0.
В дальнейшем будем полагать, что
- вершины-вообще задаются своими именами, а понятийные вершины - своими дополнительными именами; при этом игнорируется синонимия [3] и упрощаются формулировки;
- множества P(t), S(t), A(t), B(t), L(t), s(t) и a(t) содержат соответственно P, S, A, B, L, s и a элементов.
Так, для понятийной вершины t = "Карстовые озера"
| P(t) = { |
"Озера" }, |
| S(t) = { |
"Коррозионное озеро", "Провальное озеро",
"Подземные озера", "Соляные озера",
"Тектоно-карстовое озеро" }, |
| s(t) = { |
"Коррозионное озеро", "Провальное озеро" }, |
| A(t) = { |
"Варв", "Воклена", "Озерное полье" }, |
| a(t) = { |
"Варв" }, |
| B(t) = { |
"Карстовые воды" }, |
| L(t) = { |
"Карстовые источники", "Полья", "Соляной карст",
"Минеральные озера", "Подземные воды"}. |
Соответственно P = 1, S = 5, s = 2, A = 3, a = 1, B = 1, L = 5.
| W(t) = { ("Подземные озера" |
→ "Подземные воды"), |
| ("Озерное полье" |
→ "Полья"), |
| ("Тектоно-карстовое озеро" |
→ "Полья"), |
| (Соленые озера" |
→ "Соляной карст"), |
| (Соленые озера" |
→ "Минеральные озера"), |
| ("Воклена" |
→ "Карстовые источники") } |
k("Воклена") = 1,
k("Озерное полье") = 1,
k("Подземные озера") = 1,
k("Соленые озера") = 2,
k("Тектоно-карстовое озеро") = 1.
|
- Принципы визуализации фрагментов УТП
-
С точки зрения исследователя схематичное представление окрестности понятийной вершины намного предпочтительнее ее текстового описания.
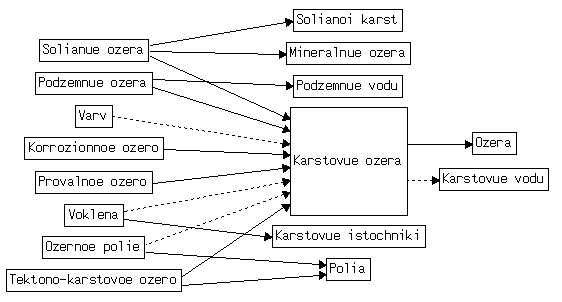
Однако попытка изобразить схему в виде классического графа (рис.2), состоящего из вершин и ребер и построенного, например, программой aiSee [4] оказывается не очень удачной.
Такой граф не обеспечивает пространственную группировку вершин в соответствии с их классификацией, что затрудняет сравнимость схем.
 |
|
Рис.2 Представление окрестности "классическим" графом |
В связи с этим предлагается принять более сложные правила визуализации, позволяющие стандартно и технологично строить схемы окрестностей. Композиционно такую схему предлагается строить вокруг прямоугольника, который символизирует раскрываемое понятие. Области над и под прямоугольником, отводятся связям "это-есть", а области справа и слева - связям "относится-к". Детали образного представления понятийной вершины t зафиксированы в семи следующих принципах:
-1- вершина t представляется прямоугольником, в верхней части которого - в шапке - размещается имя вершины, а в нижней - в подвале - ребра W(t);
-2- ребра из W(t):
- начинаются внутри прямоугольника на его границах;
- имеют вид линий, плавно меняющих направление;
- выходят за пределы прямоугольника через его левую границу;
- заканчиваются стрелками "справа-налево";
-3- родовые понятия из P(t) размещаются над прямоугольником и соединяются с ним стрелками "снизу-вверх";
-4- подвиды из S(t) размещаются под прямоугольником и соединяются с ним стрелками "снизу-вверх", причем собственные подвиды s(t) размещаются левее остальных элементов S(t);
-5- аксессуары из A(t) размещаются справа от прямоугольника и соединяются с ним стрелками "справа-налево", причем собственные аксессуары a(t) размещаются выше остальных элементов A(t);
-6- области применения из B(t) размещаются слева от прямоугольника и соединяются с ним стрелками "справа-налево";
-7- элементы множества L(t) размещаются слева от прямоугольника под элементами B(t).
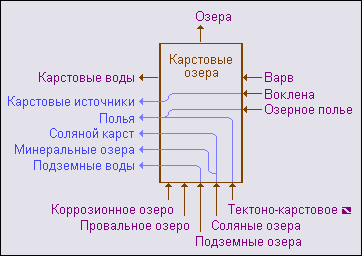 |
|
Рис. 3 Окрестность понятийной вершины "Карстовые озера" |
Схема окрестности понятийной вершины "Карстовые озера" приведена на рисунке 3.
Остановимся на принципиальных моментах алгоритма построения схем.
- Структура алгоритма визуализации
-
Алгоритм построения схем состоит из двух последовательных этапов: расчетного этапа и этапа визуализации.
 |
|
 |
|
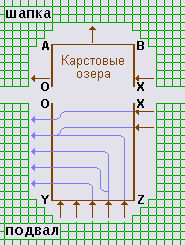
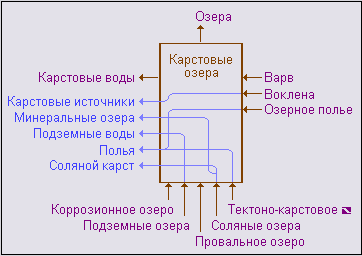
Рис.4. Шапка и подвал схемы
|
|
Рис.5. Неоптимизированный вариант схемы |
На расчетном этапе решаются четыре основных подзадачи:
-1- сортировка имен в каждой категории вершин;
-2- формирование подвала OXZY (рис.4) и размещение в нем ребер из W(t);
-3- формирование шапки ABXO (рис.4) и размещение в ней имени понятийной вершины t;
-4- формирование печатных наименований вершин.
Для формирования прямоугольника выбирается виртуальная сетка с шагом g по горизонтали и с шагом v по вертикали. Границы прямоугольника и все ребра располагаются исключительно на линиях виртуальной сетки. Ребра могут иметь вид стрелок или ломаных линий.
На этапе визуализации результаты расчетов преобразуются в графическое изображение - в файл формата GIF87. На этом этапе также решаются некоторые задачи "усовершенствования" расчетов: сглаживание ломаных, центрирование заголовка и др.
При описании алгоритма будем называть:
- парковками - точки примыкания стрелок к прямоугольнику;
- связями - отрезки вертикальных прямых, расположенных в подвале.
- Сортировка имен
-
На результирующей схеме имена вершин приводятся в линейном порядке:
- вершины из B(t), P(t), a(t) и s(t) располагаются в алфавитном порядке; а
- вершины из L(t), A(t) \ a(t) и S(t) \ s(t) располагаются в порядке, обеспечивающем максимальную наглядность связей W(t).
Остановимся на последнем условии. Если не предпринять определенных условий, то картина в подвале прямоугольника становится неоправданно громоздкой. Так, на рисунке 5 приводится неоптимизированный вариант окрестности вершины "Карстовые озера", сильно ухудшенный по сравнению с вариантом на рисунке 3. В конечном итоге, задача сортировки имен сводится к минимизации числа пересечений в подвале прямоугольника.
Сортировка вершин из L(t), A(t) \ a(t) и S(t) \ s(t) основывается на характеристиках их вхождения во множество W(t), которое состоит из компонент связности, упорядоченных по возрастанию числа ребер в каждой компоненте.
W(t) = C1 + C2 + ... + Cn, где n - число компонент.
Помимо номера каждая компонента характеризуется символьной меткой:
- если компонента связности содержит ребра, исходящие только из вершин множества A(t), то такая компонента отмечается символом "r";
- если компонента связности содержит ребра, исходящие только из вершин множества S(t), то такая компонента отмечается символом "d";
- если компонента связности содержит ребра, исходящие и из вершин A(t), и из вершин S(t), то такая компонента отмечается символом "m".
Таблица 1. Компоненты связности
| Номер | К-во ребер | Метка | Исходящие из |
| 1 | 1 | r | Воклена |
| 2 | 1 | d | Подземные озера |
| 3 | 2 | m | Озерное полье, Тектоно-карстовое ... |
| 4 | 2 | d | Соляные озера |
Для примера, приведенного на рисунке 3, множество W(t) состоит из четырех компонент связности, перечисленных в таблице 1.
Таблица 2. Характеристики вершин
| Метка | Компонента | Имя вершины |
| r | 1 | Карстовые источники |
| m | 3 | Полья |
| d | 4 | Минеральные озера |
| d | 4 | Соляной карст |
| d | 2 | Подземные воды |
| d | 2 | Подземные озера |
| d | 4 | Соленые озера |
| m | 3 | Тектоно-карстовое озеро |
| m | 3 | Озерное полье |
| r | 1 | Воклена |
| |
 |
|
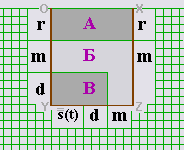
Рис.6. Правила сортировки вершин |
|
Каждая вершина из множеств L(t), A(t) \ a(t) и S(t) \ s(t) входит ровно в одну компоненту связности и, следовательно, однозначно наследует метку и номер компоненты. Унаследованные характеристики вершин из примера, приведенного на рисунке 3, указаны в таблице 2.
Замечание. Разбиение W(t) на компоненты связности является естественным, однако W(t) можно разбивать на компоненты и другими способами, конструируя при этом правило однозначного сопоставления вершин и компонент.
Элементы множества L(t) сортируются (сверху-вниз):
-1- по возрастанию меток компонент: r < m < d; а при совпадении меток
-2- по возрастанию номеров компонент; а при совпадении номеров
-3- в алфавитном порядке имен.
Элементы множества S(t) \ s(t) сортируются (слева-направо):
-1- по возрастанию меток компонент: d < m; а при совпадении меток
-2- по возрастанию номеров компонент; а при совпадении номеров
-3- в алфавитном порядке имен.
Элементы множества A(t) \ a(t) сортируются (сверху-вниз):
-1- по возрастанию меток компонент: r < m; а при совпадении меток
-2- по возрастанию номеров компонент; а при совпадении номеров
-3- в алфавитном порядке имен.
Схематично правила сортировки представлены на рисунке 6. Связи из W(t) локализуются внутри зон А, Б и В. Причем алгоритм построения гарантирует дополнительное расслоение зон А и В по числу компонент связности в каждой из них.
- Формирование подвала схемы
-
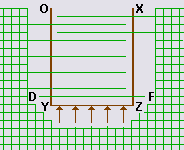
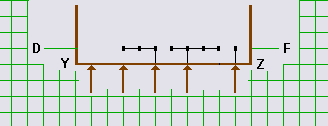
Вертикальные размеры подвала определяются числами L и A - a с учетом двух особенностей его построения (рис.7). Первая особенность состоит в том, что парковки для вершин из L(t) и A(t) \ a(t) располагаются на разных горизонталях.
Согласно второй особенности в подвале размещается дополнительная горизонталь DF, в определенном смысле дублирующая сторону YZ.
Vп = v * max(2*A - 2*a, 2*L + 1) + v
 |
|
Рис.7. Структура подвала |
Ширина подвала также зависит от двух обстоятельств:
- от начального распределения парковок для вершин S(t); и
- от количества блокировок, возникающих при размещения связей.
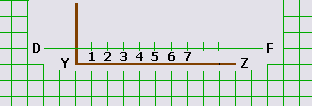
Алгоритм начального распределения парковок оперирует номерами делений виртуальной сетки (рис.8).
В результате своей работы алгоритм приписывает каждой вершине zi из S(t) = {z1, z2, ...}:
- номер ее деления-парковки на XZ; а также
- группу из k(zi) номеров:
- расположенных на DF; и
- именуемых дополнительными парковками.
| |
 |
|
Рис.8. Номера делений виртуальной сетки
|
Из соображений дизайна номера на XZ должны отличаться минимум на 2.
Множества дополнительных парковок не должны пересекаться; при этом один из номеров множества дополнительных парковок должен совпадать с номером самой парковки.
Алгоритм распределения парковок с использованием нотации языка Паскаль выглядит следующим образом:
{ Переменные i,PS,KO : integer; }
PS:=-1; { Номер последней обработанной парковки }
KO:=0; { Номер последней "занятой" доп.парковки }
for i:=1 to S do begin
PS:=max(PS+2,KO+1);
write('парковка/номер = ',i,'/',PS);
if 0 < k(zi) then begin
if PS-KO < k(zi) then KO:=KO+k(zi)
else KO:=PS;
write(' доп.парковки = ',KO-k(zi)+1,'..',KO)
end;
writeln
end;
Gп:=g*max(PS,KO) + g; { Начальная ширина подвала }
Начальное распределение парковок зависит от последовательности величин k(zi).
Приведем работу алгоритма для абстрактной последовательности 0; 0; 3; 4; 1:
парковка/номер = 1/1
парковка/номер = 2/3
парковка/номер = 3/5 доп.парковки = 3..5
парковка/номер = 4/7 доп.парковки = 6..9
парковка/номер = 5/10 доп.парковки = 10..10
Графическая интерпретация этих результатов приведена на рисунке 9.
 |
|
Рис.9. Распределение парковок |
Ширина подвала Gп, предварительно вычисленная алгоритмом распределения парковок, может увеличиваться по мере размещения в подвале ребер из W(t).
Алгоритм формирования внутренней части подвала основан на двух правилах порождения связей для ребер (w1,w2) из W(t).
Правило No.1. Если w1 из S(t), то на схему наносится связь, соединяющая свободную парковку для w1 с горизонталью для w2.
Правило No.2. Если w1 из A(t), то на схему наносится связь:
- соединяющая горизонтали для w1 и w2; и
- непересекающаяся с другими связями.
Структурно алгоритм формирования внутренней части подвала состоит из трех этапов:
Этап 1. Объявить все дополнительные парковки свободными.
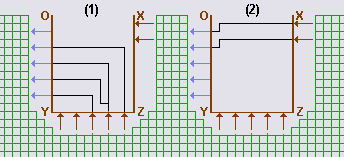
Этап 2. Применять правило No.1 до тех пор пока во множестве W(t) остаются необработанные ребра, исходящие из элементов S(t). См.рисунок 10(1). По мере построения связей свободные парковки переходят в разряд задействованных.
Этап 3. Применять правило No.2 до тех пор пока во множестве W(t) остаются необработанные ребра. См.рисунок 10(2). Если очередное применение правила No.2 оказывается заблокированным из-за отсутствия связи, "непересекающейся с другими связями", то ширина подвала увеличивается на одно деление: Gп = Gп + g.
Конец.
 |
|
Рис.10 Этапы формирования подвала схемы |
Замечание. Выбор свободной парковки и положения связи относятся к деталям реализации.
Формирование шапки схемы-
Имя понятийной вершины t состоит из некоторого количества формальных слов,
разделенных пробелами. Пробелы служат потенциальными границами в разбиении
имени на строки. Рассмотрим соотношение между возможными разбиениями имени
и начальными размерами шапки:
Gш = max(2*g*P,Gп), Vш = 2*v*max(B,a),
где Gп - вычисленная к этому моменту ширина подвала.
По известной ширине прямоугольника Wr количество строк в разбиении заданного имени S определяется однозначно. Соответствующая функция на языке Turbo Pascal имеет вид:
function Ring(S : String; Wr : integer) : integer;
var B,I,K,P : integer;
begin S:=S+' ';
Ring:=0;
P:=0; { Позиция пред.пробела }
K:=0; { Количество форм.слов }
for I:=1 to Length(S) do
if S[I] = ' ' then begin
if Wr < Wing(S,P+1,I-1) then Exit;
K:=K+1;
P:=I
end;
B:=0; { Последняя позиция пред.строки }
P:=0;
for I:=1 to Length(S) do
if S[I] = ' ' then begin
if Wr < Wing(S,B+1,I-1) then B:=P
else K:=K-1;
P:=I
end;
Ring:=K+1 end;
Функция Ring обращается к функции
Wing(C : String; H,K : integer) : integer, которая:
- вычисляет длину (в пикселах) печатного образа
подстроки C[H..K] { = Copy(C,H,K-H+1) };
- существенно зависит от особенностей выбранного шрифта.
При малых значениях Wr разместить имя невозможно, и Ring = 0. С увеличением параметра Wr количество строк в разбиении скачком достигает своего максимума, а затем ступенчато уменьшается до 1.
С практической точки зрения интерес представляет не количество строк в разбиении, а высота (в пикселах) прямоугольника, достаточного для размещения имени. В соответствии с одной из реализаций алгоритма визуализации высота прямоугольника вычисляется по формуле
высота = v * ((Ring(S,ширина) + 12) div 13)
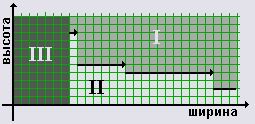
Функциональная зависимость высоты прямоугольника от заданной ширины для имени "Аэротенки для очистки сточных вод" представлена на рисунке 11.
 |
|
 |
|
Рис.11. Высота как функция ширины |
|
Рис.12. Варианты расширения |
Теоретически начальный прямоугольник Gш-на-Vш может попасть в одну из трех зон: I, II или III.
Попадание в зону I - сам график и область над ним - гарантирует размещение имени в шапке без дополнительных построений.
Попадание в зону II - строго под графиком - предполагает расширение начального прямоугольника в ширину и/или в высоту. Другими словами, необходимо выбрать экономным способом пару положительных чисел m и n таких, что (Gш + n*g)-на-(Vш + m*v) попадает в зону I.
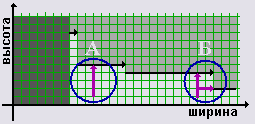
Замечание. В некоторых случаях (рис.12.A) расширение возможно единственным образом за счет увеличения высоты (n=0, m=4). В других случаях (рис.12.Б) расширение возможно двумя различными способами (n=0, m=3 или n=2, m=1). Выбор окончательного варианта определяется деталями реализации.
Попадание в зону III - область слева от графика - предполагает минимально необходимое расширение-в-ширину начального прямоугольника до попадания в зону I или II. После этого задача сводится к одному из ранее рассмотренных случаев.
Окончательно размеры прямоугольника для представления понятийной вершины определяются так:
G = Gш + n*g и V = Vп + Vш + m*v.
- Формирование печатных наименований
-
Помимо имени понятийной вершины на схему наносятся также имена других вершин УТП. При этом окончательные размеры схемы попадают в зависимость от длин этих имен. Одно или два слишком длинных имени могут существенно исказить пропорции схемы. В связи с этим алгоритм визуализации решает задачу сокращения длинных имен.
 |
|
Рис.13. Исходные данные для решения задачи сокращения имен |
Для каждой схемы задача сокращения имен решается дважды. Сначала - для правой части схемы (рис.13), а затем - для левой части, представленной на рисунке 13 только стрелками.
При сокращении имени, состоящего из q формальных слов, действуют следующие соглашения:
-1- если q ≤ 2, то имя не сокращается;
-2- если q > 2, то самый короткий вариант имени состоит из q div 2 + 1 штук начальных формальных слов и специального символа скрытого продолжения.
Буквальное следование этим соглашениям решает задачу сокращения имен не лучшим образом (рис.14). Часть из них сокращается совершенно неоправданно. Вместе с тем, воображаемое исполнение соглашений позволяет определить вертикальную границу UU (рис.14 и рис.15), соответствующую самому экономному из возможных сокращений.
 |
|
Рис.14. Самое экономное сокращение имен |
В общем случае, часть имен пресекает границу UU (рис.15). При этом можно говорить о глубине нарушения границы. Некоторые имена нарушают границу на 5 пикселов, а некоторые - на 150. Понятно, что в первом случае нужно просто отказаться от сокращения и передвинуть границу UU на 5 пикселов вправо, а во втором случае имя нужно сокращать.
 |
|
Рис.15. Имена-"нарушители"
|
Таким образом возникает известная задача формализации отношений "мало/много", для решения которой предлагается использовать аналог принципа "20/80" [5] - точку равновесия "x/100-x".
Алгоритм вычисления точки равновесия "x/100-x" (табл.3, рис.16) состоит из четырех этапов.
Этап 1. Упорядочить F штук имен, пересекающих UU, по убыванию глубин нарушений.
Этап 2. Вычислить сумму всех нарушений R[F].
Суммирование вести с фиксаций для каждого имени нарастающего итога R[I].
Этап 3. Для каждого имени вычислить значение L[I] = R[F]*I + F*R[I] - R[F]*F
Этап 4. Найти число X такое, что L[X-1] < 0 ≤ L[X].
Конец. { x ≈ (X/F)*100 % имен покрывают 100-x % нарушений }
| I | Имя | Глубина | R[I] | L[I] |
| 1 | Полная... | 147 | 147 | -174 |
| 2 | Условия... | 91 | 238 | +444 |
| 3 | Обязанность... | 9 | 247 | +734 |
| 4 | Реализация... | 7 | 254 | 1016 |
Таблица 3. Вычисление точки
равновесия
| |
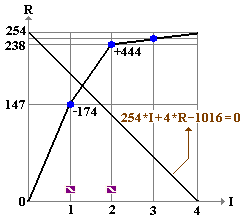 |
Рис.16. Геометрическая
интерпретация алгоритма "x/100-x" |
|
Замечание. Для примера из таблицы 3 вычисление точки равновесия как точки пересечения двух отрезков дает величину x = 1.28 (32/68).
Способ округления x до целого относится к деталям реализации алгоритма.
В описанной версии применяется округление с избытком.
 |
|
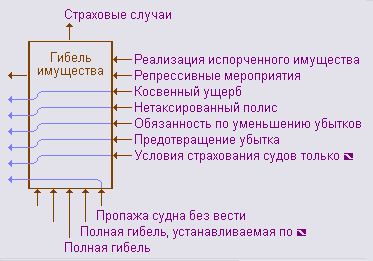
Рис.17. Результат работы процедуры сокращения имен |
Вычисленное алгоритмом "x/100-x" число X есть искомое количество имен, имеющих самые значительные нарушения длины и подлежащих сокращению до q div 2 + 1 формальных слов. Остальные F - X имен не сокращаются, они определяют окончательное положение вертикальной границы, пересекать которую имена "не имеют права".
Результат сокращения имен представлен на рисунке 17.
- Заключение
-
Алгоритм построения схем для понятийной вершины УТП реализован на сайте www.glossary.ru в качестве серверного приложения, которое динамически вызывается при обращении к функции "Формула глоссария".
Табл. 4. Закономерности построения схем
| Свойство |
Частота |
Комментарий |
A > 0 & B > 0
A = 0 & B > 0
A > 0 & B = 0
|
68%
12%
12% |
Часто схемы одновременно содержат и подвиды, и аксессуары. |
a + s = 0
a + s > 0 |
7%
93%
|
Почти все схемы содержат некоторое количество собственных
подвидов или собственных аксессуаров.
|
(0 < P) &
(0 < s < S) &
(0 < a < A) &
(0 < B) & (0 < L)
|
10% |
Только малая часть схем имеет строение общего вида. |
Наблюдение за 7351 схемами, представленными на сайте, позволяет выявить некоторые статистические закономерности в устройстве схем (таблица 4). Установлено, что эти закономерности устойчиво проявляются на всех выпусках УТП.
 |
| Рис.18. Классы схем |
Рис.19. Фрагменты рис.18 |
Соотношения между выявленными классами схем представлены на рисунке 18 и на объясняющем его рисунке 19.
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК
-
1. Гришин В.Г.
Образный анализ экспериментальных данных.
- М.: Наука, 1982. - 223с.
2. Мальковский М.Г., Соловьев С.Ю. Универсальное терминологическое пространство. Труды Международного семинара Диалог-2002 "Компьютерная лингвистика и интеллектуальные технологии", т.1. - М.: Наука, 2002, с.266-277.
www.park.glossary.ru/serios/theory01.php
3. Мальковский М.Г., Соловьев С.Ю. Методы формирования глоссариев в универсальном терминологическом пространстве. Труды Международного семинара Диалог-2003 "Компьютерная лингвистика и интеллектуальные технологии", - М.: Наука, 2003, с.438-440.
www.park.glossary.ru/serios/theory02.php
4. Программа визуализация графов aiSee: http://www.aisee.com
5. Кох Р. Принцип 80/20. - Мн.: ООО "Попурри", 2004. - 352с.
--------- * ---------
Точная ссылка:
Соловьев С.Ю.
Образные представления терминологической сети.
// Сб. Прикладное программное обеспечение.
М.: Изд-во МИРЭА, - 2008. стр.55-69.
П|р|о|д|о|л|ж|е|н|и|е ►
|
|