В работе рассматривается задача кластеризации терминологической сети и предлагается двухэтапный метод ее решения. На первом этапе отбираются кандидаты в центры кластеров, часть из них отсеивается на втором этапе, а для оставшихся центров формируются искомые кластеры. Принципы решения основных подзадач кластеризации формулируются в виде трех групп правил. Для проверки работоспособности предложенного подхода построена стратегия управления правилами, посредством которой удалось вполне успешно разделить на кластеры терминологическую сеть УТП.

 

ВВЕДЕНИЕ

Научное определение того или иного термина явно или неявно предполагает существование родственных терминов, образующих в совокупности терминосистему проблемной области [Шелов, 2003]. Структуры терминосистем представимы в виде совокупности семантических связей, допускающих объединение в единую терминологическую сеть [Мальковский и др., 2012].

Терминологическую сеть можно рассматривать как естественную (в некотором смысле) надстройку над множеством определений терминов. С формальной точки зрения терминологическая сеть представляет собой семантическую сеть, узлами которой являются определения терминов, а дугами - экземпляры бинарных отношений из заранее фиксированного набора допустимых отношений.

В терминологических сетях:

• каждая дуга представляет собой упорядоченную пару узлов, помеченную символом отношения; если для дуги не оговаривается ее родовая принадлежность, то в записи такой дуги метка опускается;
• набор допустимых отношений обязательно содержит родовидовые отношения, которым соответствуют дуги (A,B)_P, где А - вид, B - род;
• понятийным узлом называется узел в который заходит хотя бы одна дуга;
• потомками понятийного узла A называются понятийные узлы B, связанные с А дугой (B,A);
• каждый понятийный узел имеет уникальное имя, которое одновременно служит наименованием понятия;
• как правило, наименование понятия есть общее наименование объектов, составляющих его объем: "Анемометры", "Варочные печи", "Именные ценные бумаги" и т.д., но "Российская Федерация", "Ботаника" и пр.

С ростом терминологической сети увеличивается количество интегрированных в нее терминосистем, а у пользователя возникает пародоксальная, на первый взгляд, проблема потери ориентации, вызванная с нерасчлененностью сети на крупные фрагменты-кластеры. Заметим, что кластеризация имеет смысл и для всей терминологической сети, и для ее отдельных частей. Фактически кластеризация всей терминологической сети сводится к восстановлению составляющих ее терминосистем.
 

1. Подход к кластеризации

Кластеризацию терминологической сети предлагается разделить на два последовательных этапа. На первом этапе строится подмножество понятийных узлов W, именуемых кандидатами в центры кластеров. На втором этапе некоторые кандидаты из рассмотрения исключаются, а оставшиеся в множестве W центры порождают искомые кластеры.

Терминологический кластер (далее просто кластер) с центром A есть множество K(A | W), состоящее из самого узла A, а также из других узлов B, отличных от центров кластеров, но соединенных с A путем из выделенных дуг (см.раздел 2).

Каждый центр A однозначно определяет множество подчиненных ему центров S(A | W). По определению множество S(A | W) составляют узлы B из W \ { B }, соединенные выделенной дугой (B,X) с некоторым узлом X из К(A | W).

Количество узлов кластера K(A | W) будем обозначать k(A | W). Единственным параметром кластеризации является целое число MiN - минимально допустимое количество узлов в кластере.

Если W - множество кандидатов в центры кластеров, то на втором этапе кластеризации для исключения избыточных центров применяются два правила.

Правило 1.1 Исключить B из W, если (а) k(B | W) < MiN и (б) S(B | W) = ∅.

Правило 1.2 Исключить B из W, если (а) k(B | W) < MiN и (б) для всех узлов A из S(B | W) выполняется неравенство MiN ≤ k(A | W).

В результате применения каждого правила множество W изменяется: W → W_new, что порождает необходимость перевычислять после каждого применения кластеры K(A | W_new) и подчиненные центры S(A | W_new).

При анализе терминологических сетей существенно используются специальные отношения между терминами, узлами и дугами. Приведем эти отношения.

Во-первых, будем говорить, что (многословный) термин x подчинен (многословному) термину y, если термин x является развитием термина y. Примерами отношения подчиненности являются следующие пары терминов:
x = "Промышленные аварии" и y = "Аварии";
x = "Централизованная библиотечная система"
и y = "Библиотечные системы";
x = "Скорость света в вакууме" и y = "Вакуум".
Отношение подчиненности позволяет выделить в терминологической сети собственный подкласс дуг, отвечающих синтаксическому способу терминообразования [Гринев-Гриневич, 2008].

С формальной точки зрения термин x, состоящий из слов x₁, x₂, ..., x_g, подчинен термину y, состоящему из слов y₁, y₂, ..., y_h, если существует однозначная функция f : { y₁, y₂, ..., y_h } → { x₁, x₂, ..., x_g } такая, что для всех i = 1, ..., h слова y_i и f(y_i) отличаются формальными суффиксами.

Во-вторых, будем говорить, что дуга (A,B) является терминологически связанной, если имя узла А подчинено имени узла B. Из общего количества дуг, связывающих понятийные узлы, терминологически связанные дуги составляют 20%. Типичным примером дуги, не удовлетворяющей условию терминологической связанности, является дуга (A,B), в которой узлы A и B именуются "Акции" и "Ценные бумаги".

В-третьих, будем называть модельной диаграммой подсеть терминологической сети составленную из двух путей, не имеющих общих узлов, за исключением общего начала и общего конца. Общий вид модельной диаграммы представлен на рисунке 1.
 

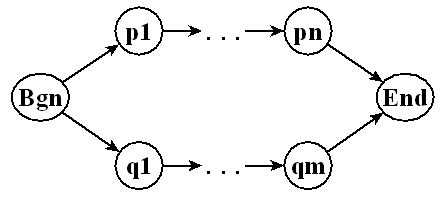Рисунок 1 - Модельная диаграмма < n,m >

Сложность модельной диаграммы есть пара целых чисел < n,m >, где n - количество внутренних узлов одного пути, а m - количество узлов второго пути, причем в такой паре всегда выполняется неравенство n ≤ m. Из двух оценок сложности < n,m > и < a,b > оценка < n,m > считается меньшей, если n + m < a + b или n + m = a + b, но n < a.

В связи с отсутствием в терминологических сетях кратных ребер, наименьшая оценка сложности модельных диаграмм есть величина < 0,1 > (рисунок 2а). А оценка, непосредственно предшествующая минимуму, есть <1,1> (рисунок 2б). Модельные диаграммы позволяют ввести оценки структурной сложности для дуг.

В-четвертых, будем называть структурной сложностью дуги минимальную сложность модельных диаграмм, содержащих эту дугу. Если дуга не входит ни в одну модельную диаграмму, то ее структурная сложность полагается равной < N,N >, где N - общее количество узлов терминологической сети. Очевидно, что структурная сложность каждой из трех дуг модельной диаграммы < 0,1 > есть величина < 0,1 >.
 

2. Выделенные дуги

Определенные сложности при кластеризации вызывают понятийные узлы, имеющие две и более исходящих дуг. При определенных обстоятельствах такой узел и все его потомки неоднократно попадают в различные кластеры, что негативно сказывается на структурных связях между кластерами. По этой причине для целей кластеризации все дуги терминологической сети подразделяются на выделенные и прочие. По определению:

• если узел имеет единственную исходящую дугу, то такая дуга является выделенной;
• если узел B имеет несколько исходящих дуг, то выделенная дуга выбирается из исходящих применением правил 2.1-2.4.

Правило 2.1 При выборе выделенной дуги отдать предпочтение терминологически связанным дугам, если таковые имеются.

Правило 2.2 При выборе выделенной дуги отдать предпочтение дугам минимальной структурной сложности.

Правило 2.3 При выборе выделенной дуги отдать предпочтение дугам (B,X), если узел X является кандидатом в центры кластеров - элементом множества W, и если такие дуги имеются.

Правило 2.4 При выборе выделенной дуги отдать предпочтение родовидовым связям, то есть дугам (B,X)_P, если таковые имеются.

Правила 2.1-2.4 устроены таким образом, что они сокращают число исходящих дуг, претендующих стать выделенными. В худшем случае, когда правило не находит предпочтительных дуг, состав претендентов не изменяется. Для практического использования правил необходимо установить порядок их применения.
 

3. Центры кластеров

Исследования по терминоведению, а также анализ терминологических сетей выявили некоторое количество свойств-закономерностей присущих терминосистемам [Шелов, 2003], [Мальковский и др., 2013]. При обнаружении центров кластеров свойства терминосистем используются в иной роли - в роли правил обнаружения терминосистем. Перемена местами посылок и следствий не проходит бесследно. Построенные из закономерностей правила кластеризации порождают определенное количество ложных центров, а в некоторых случаях вообще не позволяют выявить имеющийся (истинный) центр кластера. В связи с этим для построения множества W кандидатов в центры искомых кластеров предлагаются несколько взаимодополняющих правил.

Правило 3.1 Квалифицировать узел X как возможный центр кластера, если в терминологической сети существуют терминологические дуги (B,X).
 

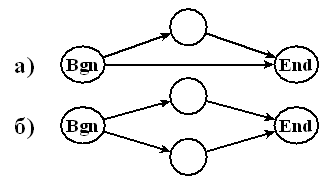Рисунок 2 - Модельные диаграммы < 0,1 > и < 1,1 >

Правило 3.2 Квалифицировать узел X как возможный центр кластера, если X является концевым узлом End в некоторой модельной диаграмме структурной сложности <0,1> (см. рисунок 2a).

Правило 3.3 Квалифицировать узел X как возможный центр кластера, если X является концевым узлом End в некоторой модельной диаграмме структурной сложности <1,1> (см. рисунок 2б).

Правило 3.4 Квалифицировать узел X как возможный центр кластера, если в терминологической сети найдутся по крайней мере три дуги (A,X)_P, (B,X)_P и (C,X).

Правило 3.5 Квалифицировать узел X как возможный центр кластера, если X не имеет исходящих дуг.

Правила 3.1-3.5 набирают кандидатов в центры кластеров. Следующие два правила отбраковывают заведомо непригодных кандидатов.

Правило 3.6 Исключить узел X из состава кандидатов в центры кластеров, если в X имеет три и менее потомков.

Правило 3.7 Исключить узел X из состава кандидатов в центры кластеров, если в терминологической сети найдутся - см. рисунок 3 - три дуги (A,X), (B,X) и (X,C) такие, что

• A, B, C - понятийные узлы;
• дуга (X,C) не является терминологически связанной; однако
• имя узла A подчинено имени узла C;
• имя узла B подчинено имени узла C.

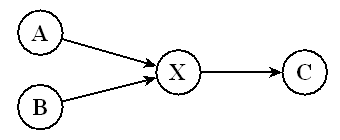Рисунок 3 - Терминологически связанный фрагмент

Последнее правило применимо, например, в ситуации, когда
имя А есть "Атмосферное давление",
имя B есть "Атмосферные осадки",
имя X есть "Метеорологические элементы",
имя C есть "Атмосфера".
Здесь понятие X "блокирует" синтаксические связи меду терминами А и С, а также между B и C, хотя A, B и С несомненно принадлежат одному терминологическому кластеру.
 

4. Алгоритм кластеризации УТП

Любой алгоритм кластеризации, построенный на базе правил кластеризации, реализует тот или иной порядок их выполнения. Работоспособности предложенного подхода подтверждается алгоритмом кластеризации терминологической сети УТП [Мальковский и др., 2012], насчитывающей около 10 тысяч понятийных узлов. В качестве исходных данных алгоритм использует собственно УТП и целочисленный параметр MiN. Результатом работы алгоритма является набор терминологических кластеров. Двухэтапная организация вычислений имеет вид:

Этап 1. Последовательно построить:

• множество W₁ с помощью правила 3.1;
• множество W₂ с помощью правила 3.2;
• множество W₁₂ = W₁ ∪ W₂;
• множество W₃ с помощью правила 3.3;
• множество W₄ с помощью правила 3.4;
• множество W₃₄ = W₃ ∪ W₄;
• множество W₅ с помощью правила 3.5;
• множество W₆ с помощью правила 3.6;
• множество W₇ с помощью правила 3.7;
• множество кандидатов в центры кластеров W = ((W₁₂ ∩ W₃₄) ∪ W₅) \ (W₆ ∪ W₇).

Этап 2. Последовательно выполнить действия:

• исключить из W часть кандидатов в центры кластеров посредством правила 1.1;
• исключить из W часть кандидатов в центры кластеров посредством правила 1.2;
• для каждого центра B, сохранившегося в W, построить терминологические кластеры K(B|W).

Процедура построения выделенных дуг, неявно задействованная на втором этапе, последовательно применяет к набору исходящих дуг правило 2.1, правило 2.2, правило 2.3 и, наконец, правило 2.4. Искомая выделенная дуга считается построенной, если после применения очередного правила множество исходящих дуг сократилось до одной дуги.

Метод построения терминологической сети УТП позволяет (хотя и с оговорками) проследить происхождение терминов, а значит, позволяет выявить истинные кластеры, пригодные для проверки результатов кластеризации.

Множества W₁₂ и W₃₄, построенные на первом этапе, содержат практически идентичные подмножества центров истинных кластеров, однако сильно различаются в части ложных центров. По этой причине их пересечение, фигурирующее в окончательном вычислении W, позволяет избавиться от значительного количества (от 50%) ложных центров.

По результатам проверки алгоритма кластеризации УТП установлено, что при MiN = 19 подтверждаются около 90% истинных кластеров, а остальные 10% кластеров нуждаются в дополнительном анализе.
 

Заключение

Важнейшей особенностью описанных правил кластеризации является их интерпретируемость, что позволяет создавать алгоритмы кластеризации с заданными свойствами.

Вообще говоря, особенности кластеризации существенно зависят от выбора конкретной терминологической сети. Вместе с тем, подход к кластеризации через постулирование закономерностей позволяет надеяться, что однажды построенный алгоритм будет вполне устойчив к изменениям сети. По этой причине разработка универсального алгоритма кластеризации представляется необязательной.
 

Библиографический список

[Гринев-Гриневич, 2008] Терминоведение / С.В.Гринев-Гриневич - М.: Академия, 2008.

[Мальковский и др., 2012] Мальковский М.Г., Терминологические сети / M.Г.Мальковский, С.Ю.Соловьев // OSTIS-2012. Материалы конференции. С. 77-82
www.park.glossary.ru/serios/theory10.php

[Мальковский и др., 2012] Мальковский М.Г., Исследование родовидовых отношений в терминологических сетях / M.Г.Мальковский, С.Ю.Соловьев // OSTIS-2013. Материалы конференции. С. 147-152
www.park.glossary.ru/serios/theory11.php

[Шелов, 2003] Термин. Терминологичность. Терминологические определения / С.Д.Шелов - СПб.: Филологический факультет СПбГУ, 2003.

--------- * ---------

Точная ссылка: Мальковский М.Г., Соловьев С.Ю.
Правила формирования терминологических кластеров.
// Материалы IV Международной научно-технической конференции
"Открытые семантические технологии проектирования интеллектуальных систем (OSTIS-2014)"
- Минск: БГУИР, 2014. С.169-172

Copyright ©
2000-2022
Web-and-Press